こんばんは。
ゼロからディープラーニングを勉強してみる第3弾で、今回は無謀にもExcelで畳み込みニューラルネットワークを組んで実験してみます。
手書き数字のMNISTデータセットを使って畳み込み層やMaxプーリング層を組んだり、ニューロンを増やしたり、画像を圧縮したり、活性化関数を変えたり、いろいろ実験しました。
ディープラーニングはとにかくCPUタスクと膨大な時間がことごとく奪われるということがよ~く分かりましたよ。スーパーコンピューターが必要になる理由も理解できました。
畳み込みニューラルネットワークは英語でConvolutional Neural Network (略してCNN) というらしいです。
とある参考書とかネットの情報では、「畳み込み」という言葉ではなく、いきなりConvolutionという単語が出てくるところがあって、「日本語で書け!!!」と言いたくなることが多々ありましたね。
でも、今回の実験でしばらく使っていると、この専門用語もだんだん慣れてきました。
こうやって素人だった自分も専門用語が多くなってしまうんだなとつくづく思いました。
前回記事の簡単なニューラルネットワークでは、ごく少量の9画素しか扱いませんでしたが、畳み込みニューラルネットワークを使うと、多量の画素でも効率良くニューラルネットワークが組めるようになるとのことです。
つい最近知ったのですが、ディープラーニングとは、この畳み込みニューラルネットワークで学習することを言うらしいですね。
だんだん核心に近づいて来ましたよ!
今回はExcelで自分なりに試行錯誤して、かなりの回数をガッツリとディープラーニングしてみました。
ツールを使うよりも、Excelでやることによって理解が視覚的に一層深まりましたよ。
ちょっと前までは、AIやディープラーニング、機械学習、ニューラルネットワークなどの用語について区別できませんでしたが、それもようやく分かってきた感じです。
ディープラーニングって、実際に自分で動かしてみて初めて理解するもんなんですね。
因みに過去2回、Excelでディープラーニングを勉強した経緯をブログで書いているので、初めてこの記事を見る方は、以下のリンクも参照してください。
ゼロからディープラーニングを勉強してみる ~Excel編その1。自己流計算式の限界とバイアス、シグモイド関数について~
ゼロからディープラーニングを勉強してみる ~Excel編その2。ニューラルネットワークと学習~
今回は最長30時間という計算時間を要したことがありました。
その間、Excelが一切使えなくなるので、かなり支障をきたしました。
それに、無知ゆえにずーっと間違えていることに気付かず、ひたすら長時間ディープラーニングしていたこともありました。
最終的にソフトマックス関数を使わなかったことが原因だったのですが、今回の実験で失敗も含めて様々なことを試せたので、おかげでディープラーニングの主なパラメータの特徴を肌で感じることができました。
では、これから今回やった実験を紹介してみます。
Microsoft Excel の計算式がある程度使えることを前提としています。
因みに私はこの分野はド素人ですので、間違えたり勘違いしていることも多々あります。
ソースコードやExcelファイルも動作保証しません。
ただ、何かお気づきの点があればコメント投稿等でご連絡いただけると幸いです。
- 学習用の手書き数字データセットMNISTをExcel表に取り込む
- 畳み込みニューラルネットワークを作ってみる
- 学習後の重みと畳み込み演算の不思議
- 学習データを約10倍増やしてみる
- 画像を前処理で圧縮して出力層を増やしてみる
- 畳み込み層のニューロン(ノード)を増やす
- 活性化関数にtanhを使ってみる
- 出力層のシグモイド関数をソフトマックス関数に変更してみる
- Excelで計算するディープラーニングの限界
- まとめ
【目次】
参考書籍
前回記事同様、主に以下の書籍を参考にしました。
初めてディープラーニングを学ぶ人にはとにかくお勧めです。
【電子書籍Kindle版】
【書籍版】
【題名】
Excelでわかるディープラーニング超入門
【著者】
涌井 良幸、涌井 貞美
【出版社】
株式会社技術評論社
自己流サンプルファイル
今回作った自己流のExcelファイルはGitHubの以下のリンクに置いておきます。
マクロは入れていません。
https://github.com/mgo-tec/test_excel_deeplearning
※ファイルの容量がメチャメチャ大きいものがあります。
まとめてダウンロードせずに、ファイルを1つずつダウンロードした方が良いです。
ダウンロードに相当な時間がかかることをご了承下さい。
1.学習用の手書き数字データセットMNISTをExcel表に取り込む
さて、まず、教師用、学習用のデータが無ければ話になりません。
本当はイメージセンサからの実際の画像データをExcel表にしたかったのですが、ちょっと難しいので、ディープラーニング界隈で有名な無料で使用できる学習データMNISTというものを題材にしていきます。
MNISTとは、Modified National Institute of Standards and Technology database の略だそうですが、最初に紹介した書籍「Excelでわかるディープラーニング超入門」では、
Mixed National Institute of Standards and Technology となっています。さて、どちらが正しいのかな?
それは、Yann LeCun氏、Corinna Cortes氏、Christopher J.C. Burges氏によって作られた0~9の手書き数字データセットで、28×28 pixel の白黒データ60,000枚の学習データと10,000枚のテスト用データがあります。
ライセンス表記が見当たらなかったのですが、ネットの情報ではCC0ライセンスらしいです。
先に紹介した参考書籍「Excelでわかるディープラーニング超入門」では、このMNISTデータセットを9×9 pixelデータに移植したものを使っています。
しかし、今回の私の実験では、28×28 pixelデータをそのまま使ってみたかったので、参考書には無いことにいきなり取り組んでみます。
そのまま独自にExcel表に変換してみたのでそれを紹介してみます。
これは前回記事で使ったような3×3 pixelのデータとは比較にならないほど膨大なデータです。
1-1. MNISTデータのダウンロード
MNISTデータセットは以下のサイトで、ダウンロードできます。
http://yann.lecun.com/exdb/mnist/
そのサイトのページの上部に以下のファイルのリンクがあります。
train-images-idx3-ubyte.gz
train-labels-idx1-ubyte.gz
t10k-images-idx3-ubyte.gz
t10k-labels-idx1-ubyte.gz
そのリンクを右クリックしてダウンロードできます。
これはgz形式で圧縮されているので、専用の解凍ソフトが必要です。
Windows10 の場合、7-Zip などのソフトを使って解凍すれば良いと思います。
解凍すると以下のファイルになります。(拡張子無し)
train-images.idx3-ubyte (学習用画像データ60000枚 45,938KB)
train-labels.idx1-ubyte (学習用ラベルデータ 59KB)
t10k-images.idx3-ubyte (テスト用画像データ10000枚 7,657KB)
t10k-labels.idx1-ubyte (テスト用ラベルデータ 10KB)
1-2. MNISTデータをマクロ(VBA)でExcel表に取り込む
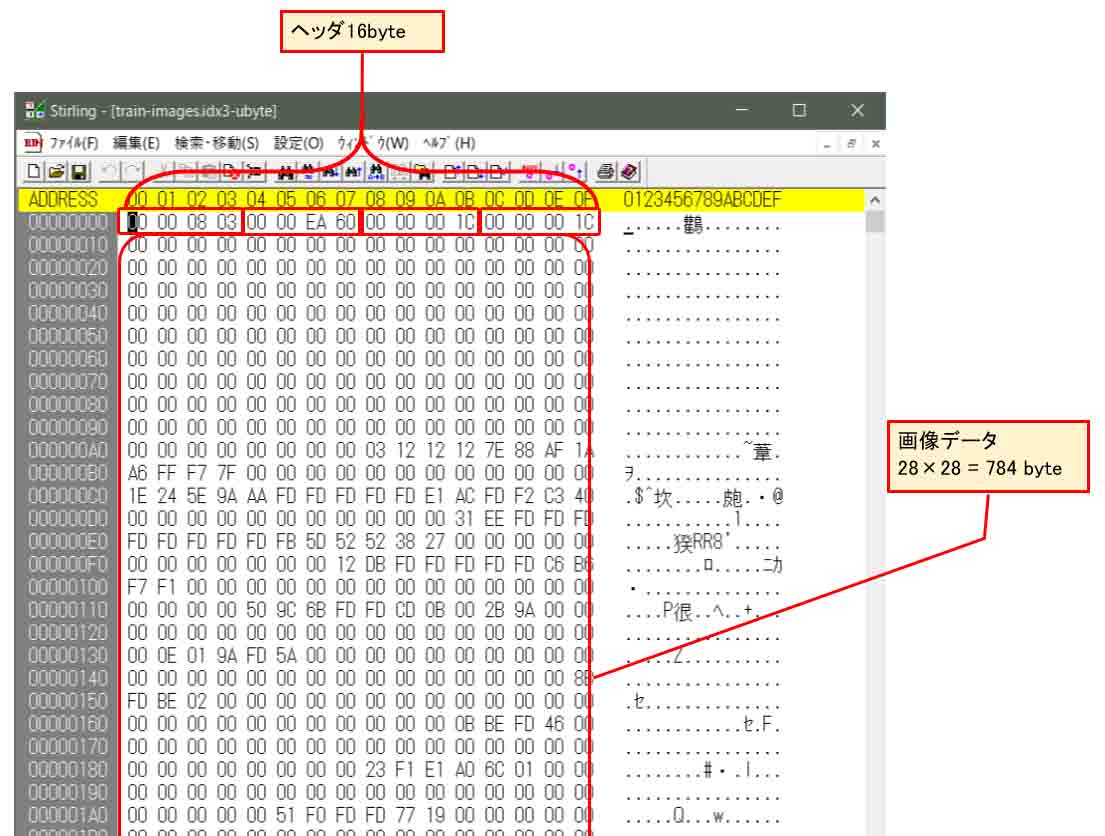
先にダウンロードして解凍したMNISTの画像データ(train-images.idx3-ubyte)をStirlingなどのバイナリエディタで開いてみると、以下のようになります。
(図01-01)
このように、最初の16byteがヘッダ情報です。
①4byte (32bit): マジックナンバー(独自に割り当てられた数値)
②4byte (32bit): データ数(0xEA60 = 60000)
③4byte (32bit): 画像の水平画素数(0x1C = 28)
④4byte (32bit): 画像の垂直画素数(0x1C = 28)
その後が28×28 pixel の画像データ60000枚が連続しています。
28×28 = 784 byte ごとのデータになっています。
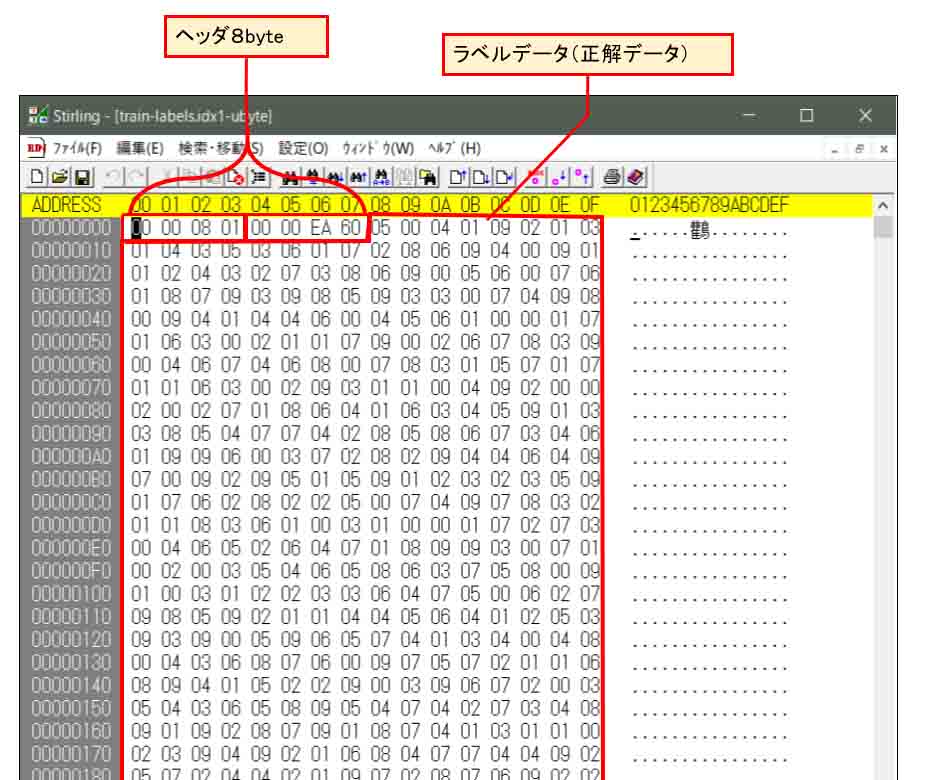
そして、学習用ラベルデータファイル(train-labels.idx1-ubyte)には、手書き画像データの正解データが入っています。
Stirlingなどのバイナリエディタで開いてみると、こんな感じです。
(図01-02)
このように、最初の8byteがヘッダ情報です。
①4byte (32bit): マジックナンバー(独自に割り当てられた数値)
②4byte (32bit): データ数(0x0000EA60 = 60000)
その後1byteごとに画像データと同じ順番で正解データが入っています。
つまり、0~9の数値ですね。
5, 0, 4, 1, 9,……etc
という感じに並んでいます。
ヘッダ情報は今回は不要なので、画像データとラベルデータの実データ部分を最低200パターンくらいはExcel表に取り込みたいわけです。
手入力なんてことは絶対やりたくありません。
そこで、Excel のマクロ(VBA)でプログラミングして取り込んでみたいと思います。
VBAは昔ちょっといじったくらいで殆ど使ったことがありませんでした。
最近はArduinoでC/C++ くらいしか使っていないので、ちょっと手間取りました。
独特なコーディング規約や命名規則があるらしく、ネットの情報をあさってみました。
そしたら、以下のサイトにとっても有効な情報がありました。
VBAでバイナリファイルを読み込む(一括、1バイト、指定バイト)
vbabeginerさんに感謝感謝です。
そのサイトを参考に、以下のように自分なりにプログラミングしてみました。
Sub ReadBinaryFile()
Dim strImageFilePath As String '// Imageファイルパス
Dim strLabelFilePath As String '// labelファイルパス
Dim fnImage '// ラベルファイル番号
Dim fnLabel '// ラベルファイル番号
Dim bytArray() As Byte '// 読み込み画像データ配列
Dim bytHeadArray() As Byte '// 読み込みヘッダデータ配列
Dim bytTmpData As Byte '// 読み込み一時データ
Dim lngArySize As Long '// 画像配列サイズ
Dim lngAryHeadSize As Long '// ヘッダ配列サイズ
Dim lngFileSize As Long '// ファイルサイズ
Dim i As Long '// ループカウンタ
Dim j As Long '// ループカウンタ
Dim k As Long '// ループカウンタ
Dim lngSeakAry As Long '// 配列のシーク位置
Dim lngCursorCellX As Long '//セル列カーソル位置
Dim lngCursorCellY As Long '//セル行カーソル位置
Dim lngCursorCount As Long
Dim lngMaxNum As Long '//読み込みパターン最大数
Dim blnUseNumArray() As Boolean '//使う数値判定のための配列
'// ラベルファイルパス設定
strLabelFilePath = "D:\xxxxxx\xxxxxx\train-labels.idx1-ubyte"
'// 画像ファイルパス設定
strImageFilePath = "D:\xxxxxx\xxxxxx\train-images.idx3-ubyte"
'//読み込みパターン最大数
lngMaxNum = 1000
'-------まず、Labelデータを開いて、正解データをセルに書き込む------------------------
'// Labelファイル番号取得
fnLabel = FreeFile
'// Labelファイルオープン
Open strLabelFilePath For Binary Access Read As #fnLabel
'// ファイルサイズ取得
lngFileSize = LOF(fnLabel)
'// Labelデータ配列領域確保
lngAryHeadSize = 8 '//headerサイズ
ReDim bytHeadArray(0 To lngAryHeadSize - 1)
lngArySize = lngMaxNum
ReDim bytArray(0 To lngArySize - 1)
ReDim blnUseNumArray(0 To lngMaxNum - 1)
'// Labelデータ配列サイズ分を読み込み
Get #fnLabel, , bytHeadArray
Get #fnLabel, , bytArray
lngCursorCellY = 7
lngSeakAry = 0
lngCursorCount = 0
For i = 0 To lngArySize - 1
'// 配列から1バイト取得
bytTmpData = bytArray(i)
Select Case bytTmpData
'// 出力
Case 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
blnUseNumArray(i) = True
lngCursorCellY = (lngCursorCount * 30) + 7
Worksheets("Sheet1").Cells(lngCursorCellY, 33).Value = bytTmpData
lngCursorCount = lngCursorCount + 1
Case Else
blnUseNumArray(i) = False
End Select
Next i
'// ファイルクローズ
Close #fnLabel
'-----------Image画像ファイル読み込み、28x28セルに書き込む--------------------------
'// Imageファイル番号取得
fnImage = FreeFile
'// Imageファイルオープン
Open strImageFilePath For Binary Access Read As #fnImage
'// ファイルサイズ取得
lngFileSize = LOF(fnImage)
'// Imageデータ配列領域確保
lngAryHeadSize = 16 '//headerサイズ
ReDim bytHeadArray(0 To lngAryHeadSize - 1)
lngArySize = 28 * 28
ReDim bytArray(0 To lngArySize - 1)
'// Imageデータ配列サイズ分を読み込み
Get #fnImage, , bytHeadArray
For i = 0 To lngAryHeadSize - 1
'// 配列から1バイト取得
bytTmpData = bytHeadArray(i)
'// Imageデータヘッダ情報をセルに出力
Worksheets("Sheet1").Cells(2, i + 3).Value = i
Worksheets("Sheet1").Cells(3, i + 3).Value = bytTmpData
Next i
lngCursorCellY = 6
'// 画像データを読み込んでセルに出力
For k = 1 To lngMaxNum
'// Imageデータを配列サイズ分を読み込み
Get #fnImage, , bytArray
If blnUseNumArray(k - 1) = True Then
For i = 1 To 28
'// セルに1~28のインデックスを出力
Worksheets("Sheet1").Cells(lngCursorCellY, i + 2).Value = i
Worksheets("Sheet1").Cells(lngCursorCellY + i, 2).Value = i
Next i
lngCursorCellY = lngCursorCellY + 1
lngSeakAry = 0
For j = 0 To 27
For i = 0 To 27
'// 配列から1バイト取得
bytTmpData = bytArray(lngSeakAry)
lngSeakAry = lngSeakAry + 1
'// 画像データをセルに出力
Worksheets("Sheet1").Cells(lngCursorCellY, i + 3).Value = bytTmpData
Next i
lngCursorCellY = lngCursorCellY + 1
Next j
lngCursorCellY = lngCursorCellY + 1
End If
Next k
'// ファイルクローズ
Close #fnImage
End Sub
これは、0から9までの文字全てを変換するプログラムです。
MNISTの画像データとラベルデータファイルから抽出します。
24行と26行のところは、自分で保存したMNISTデータファイルのパスに書き換えます。
また、一部の文字だけ抽出したい場合は、59行目のCase文の数値を書き換えればOKです。
例えば、2と3と5だけ抽出したい場合は、
Case 2, 3, 5
とすればOKです。
VBAは変数名の決め方が独特ですね。
プリフィックスという変数の型名に相当するもの(str, byt, lngなど)を前に記述しています。
ただ、これは無くても良いらしいのですが、プログラミング最中に予約語候補がポップアップで表示されて、予約された関数名や変数名と被ることがあるので、私の場合はプリフィックスを使ってみました。
そして、配列の宣言もC言語と違って独特ですね。
このコードが正しいのかどうかは正直分かりませんが、とりあえず期待する動作になったのでヨシとします。
strLabelFilePath はラベルデータファイル、つまり、正解データの入っているファイルのパスを入力します。
strImageFilePath は画像データのファイルパスを入力します。
lngMaxNum で学習データの最大パターン数を決めています。
ここでは1000個としました。
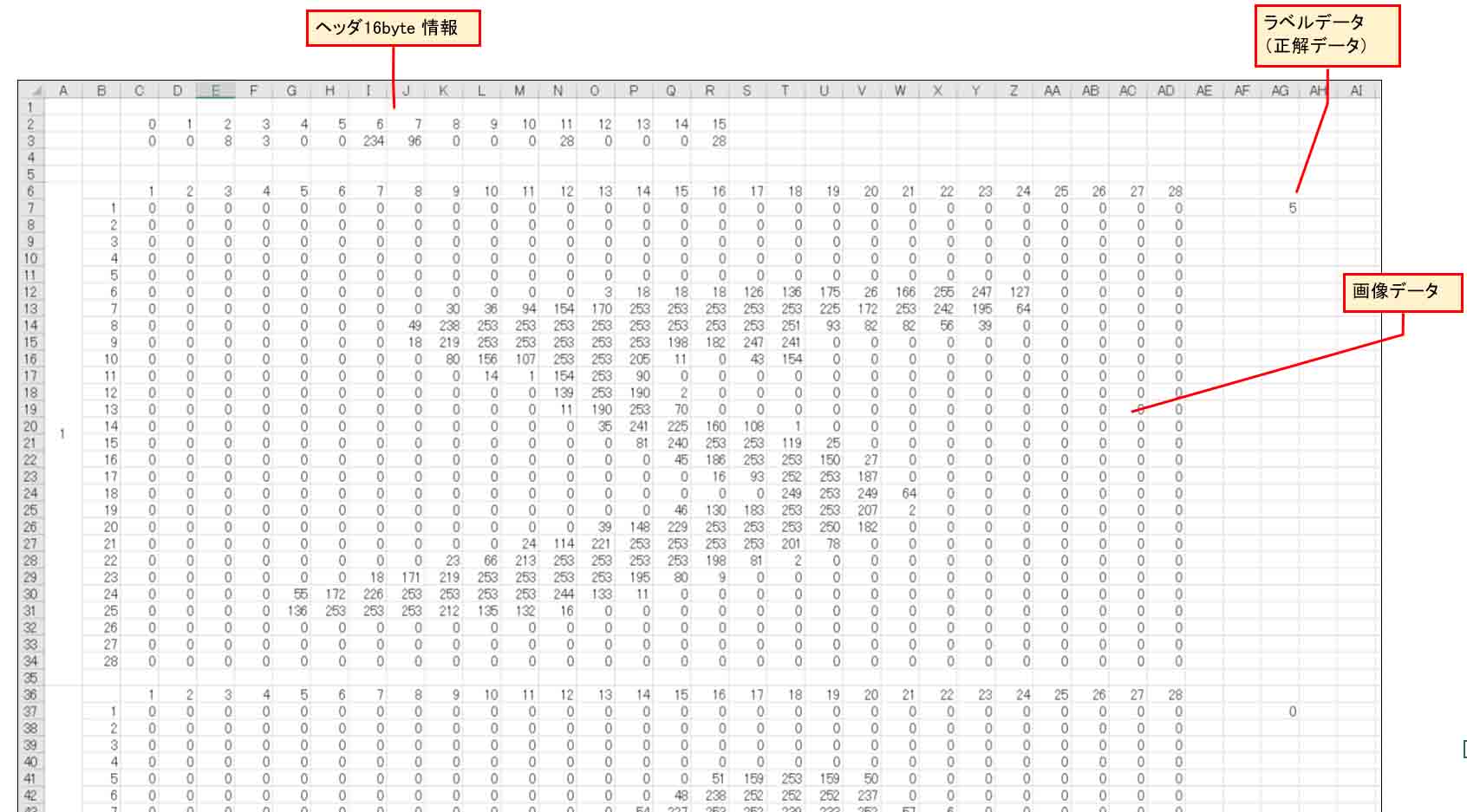
このマクロを実行すると、Sheet1に以下のように出力されます。
(図01-03)
因みに、1000のデータを変換するのに、私のパソコン環境では1分弱かかりました。
ということは、60,000のデータを変換しようとすると、単純計算でその60倍かかるとして、合計1時間かかる計算になります。
ただ、今回、60,000データを変換していたら10時間以上たっても終わらず、途中でエラーになって止まってしまいました。
実は、裏でWindowsアップデートがかかっていて、Excelが停止してしまったようです。
又は、1ファイル中の容量をオーバーしてしまったのかも知れません。
いずれにしても、Excelで60,000ものMNISTデータを扱うのは途方もない計算時間がかかるので、やめておいた方が無難です。
そんなわけで、今回はデータ数1000個を標準として、多くても10,000個までのデータを扱って学習させていきます。
このデータは最小に紹介したGitHubの中に以下のファイルで置いておきます。
これはマクロ無しブックです。
training_data_(0-9)1000.xlsx
マクロが入っているとウィルスソフトに弾かれてしまうので、あえて外してあります。
マクロが必要な場合は、上のソースコードをマクロにコピー&ペーストすれば良いです。
1-3. MNISTデータを実画像っぽく視覚化してみる
因みに、もっとイメージ的に分かり易いようにするために、この数値データをセルの背景色に置き換えるマクロ(VBA)も作ってみました。
新たにSheet2を作成して、以下のコードを実行させます。
Sub DisplayPixelImage()
Dim bytTmpData As Byte
Dim i As Long
Dim j As Long
Dim k As Long
Dim lngXcel As Long
Dim lngYcel As Long
Dim lngStartXcel As Long
Dim lngPixSize As Long
Dim lngMax As Long
lngPixSize = 28 '//1辺のピクセル数
lngMax = 1000 '//変換データ最大数
lngStartXcel = 3
lngXcel = lngStartXcel
lngYcel = 7
bytTmpData = 0
For k = 1 To lngMax
'//正解ラベルデータの取得と表示
Worksheets("Sheet2").Cells(lngYcel, 33).Value = Worksheets("Sheet1").Cells(lngYcel, 33).Value
'//画像データ表示
For j = 1 To lngPixSize
For i = 1 To lngPixSize
bytTmpData = Worksheets("Sheet1").Cells(lngYcel, lngXcel).Value
Worksheets("Sheet2").Cells(lngYcel, lngXcel).Interior.Color = RGB(bytTmpData, bytTmpData, bytTmpData)
lngXcel = lngXcel + 1
Next i
lngXcel = lngStartXcel
lngYcel = lngYcel + 1
Next j
lngYcel = lngYcel + 2
Next k
End Sub
すると、Sheet2にこんな感じで表示されます。
(図01-04)
よりMNISTデータの様子が分かり易くなって、手書きっぽい感じが表現されていてバッチリです。
以上の出力データは、最初に紹介したGitHubのところに、
pixel_image(all)1000.xlsx
というExcelファイルを置いておきます。
マクロを入れるとウィルスソフトで弾かれてしまうので、マクロ無しブックです。
マクロはご自分で入れてください。
2.畳み込みニューラルネットワークを作ってみる
では、先ほど作ったMNISTのExcelデータから、畳み込みニューラルネットワーク(CNN)を作ってみます。
ところで、YouTubeにSONYのDeep Learning入門動画があります。
https://www.youtube.com/watch?v=OwccN7rj4Qg
その動画には、やたらとConvolutionとかMaxPoolingとか出て来て、最初見た時には入門にしては全く意味わからなかったんです。
ですが、今回の実験でようやく分かるようになってきました。
では、先ほど紹介した参考書籍「Excelでわかるディープラーニング超入門」を参考にしながら、独自に組んでみます。
その参考書では9×9 pixel の画像データを扱っていますが、ここでは無謀にもいきなり 28 x 28 pixel で挑戦してみます。
なぜかというと、MNISTの手書きデータを加工せずにそのまま使ってみたかったからです。
28×28 pixel ではデータが膨大なので、参考書籍にあるように畳み込み層が1つではとても無理ですから、今回は畳み込み層を2つ作って圧縮してみます。
2-1. 1つ目の畳み込み層を作る
まず、1つめの畳み込み層(Convolution)を作ってみます。
まず、新たなExcelファイルを作り、「学習データ」という名前のシートを作成しておきます。
そして、先の1章で作ったExcel版MNISTデータを使いたいところですが、実はExcelのソルバーの制約上、0~9のすべての手書き数字を扱うことはできません。
これは後々この記事を読み進めていくと分かって来ます。
よって、まずここでは2と5の手書き数字だけを抽出します。
1章のマクロ(VBA)の59行目のCase文を修正して、
Case 2, 5
として、マクロを実行させます。
そして、出力されたExcelデータを丸々コピー&ペーストします。
合計で191データあると思います。
このExcelデータは、先ほど述べたGitHubに
cnn(2,5)_p_1000.xlsx
というファイル名で置いておきます。
次に、新しいシートを作成し、「学習計算」というシート名に変えておきます。
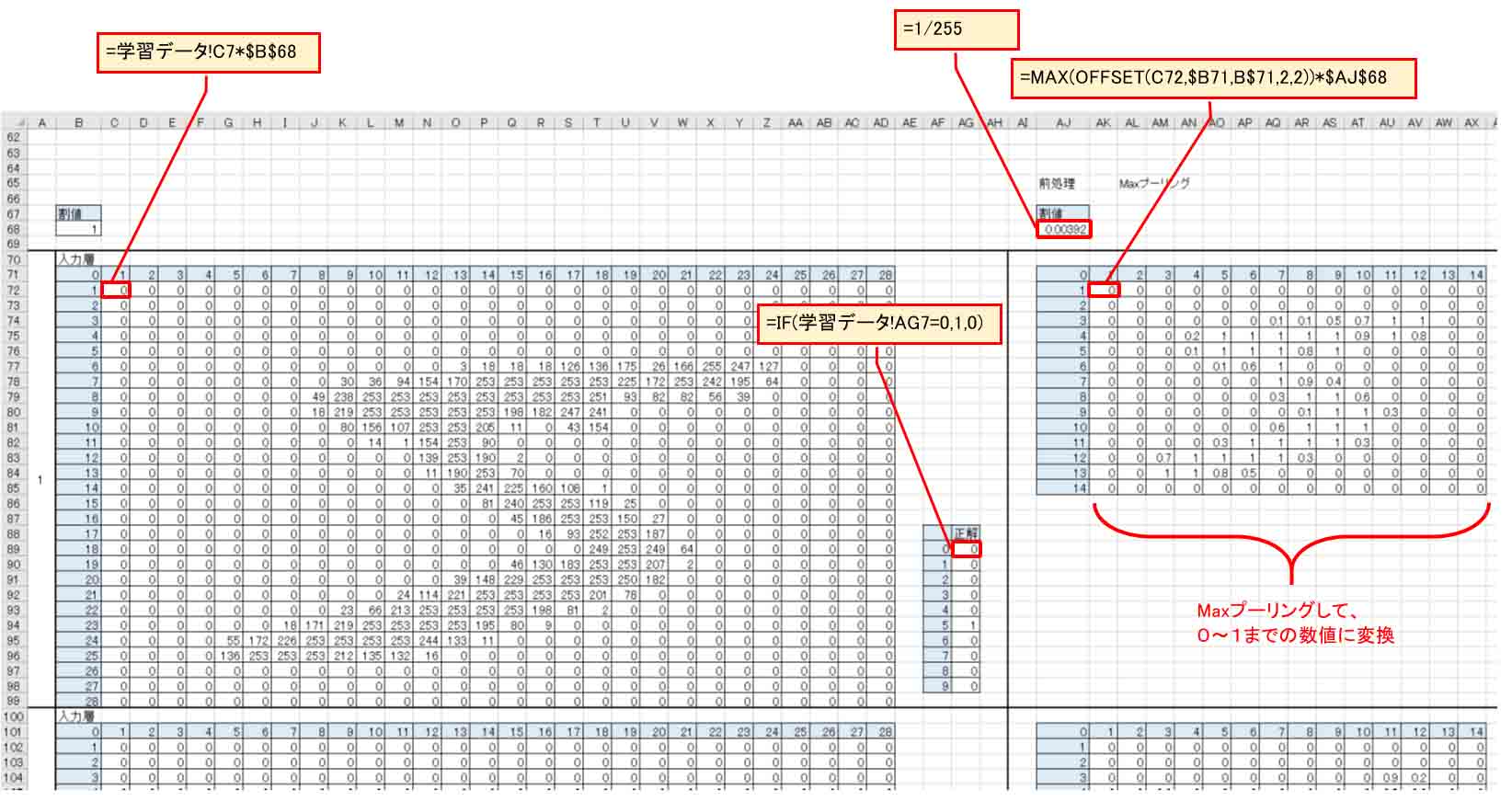
その「学習計算」シートに「学習データ」シートとリンクさせて、下図の様な表を作成します。
これをニューラルネットワークの入力層とします。
(図02-01)
入力層のニューロンは、28×28 = 784個という膨大な数です。
前回記事の9個のニューロンとは比べ物にならないほど巨大ですね。
Excelのソルバーは200までのパラメータしか扱えないので、これではとても無理です。
そこで、畳み込みニューラルネットワークを作って、圧縮していきます。
まず、各ニューロンの値は0~255という範囲で、学習計算に使うソルバー計算には不向きなため、0~1の範囲に収めるため、すべてのニューロンを255で割ります。
ただし、割り算は計算が遅いので、掛け算にしたいです。
つまり、1/255 = 約0.00392 という値を絶対参照にして、各ニューロンに掛けるようにしました。
適当な名前が思い付かなかったので、「割値」としました。「掛け値」でも良かったかも知れませんね。
書籍「Excelでわかるディープラーニング超入門」では0.01を掛けていますが、自分としては0~1に収めるという方が良いかなと思いました。
そして、ラベルファイルからの正解データは、上図のようにIF文で欄を作っておきます。
正解がゼロの欄は
=IF(学習データ!AG7=0,1,0)
正解が1の欄は
=IF(学習データ!AG7=1,1,0)
・・・・・・・
としておきます。
次に、いよいよ畳み込み層を作っていきます。
専門用語では Convolutionです。
先にも述べたように、ディープラーニングの参考書では嫌になるほど出てくる用語です。
意味が解らなくても、まずは参考書どおりに作ってみます。
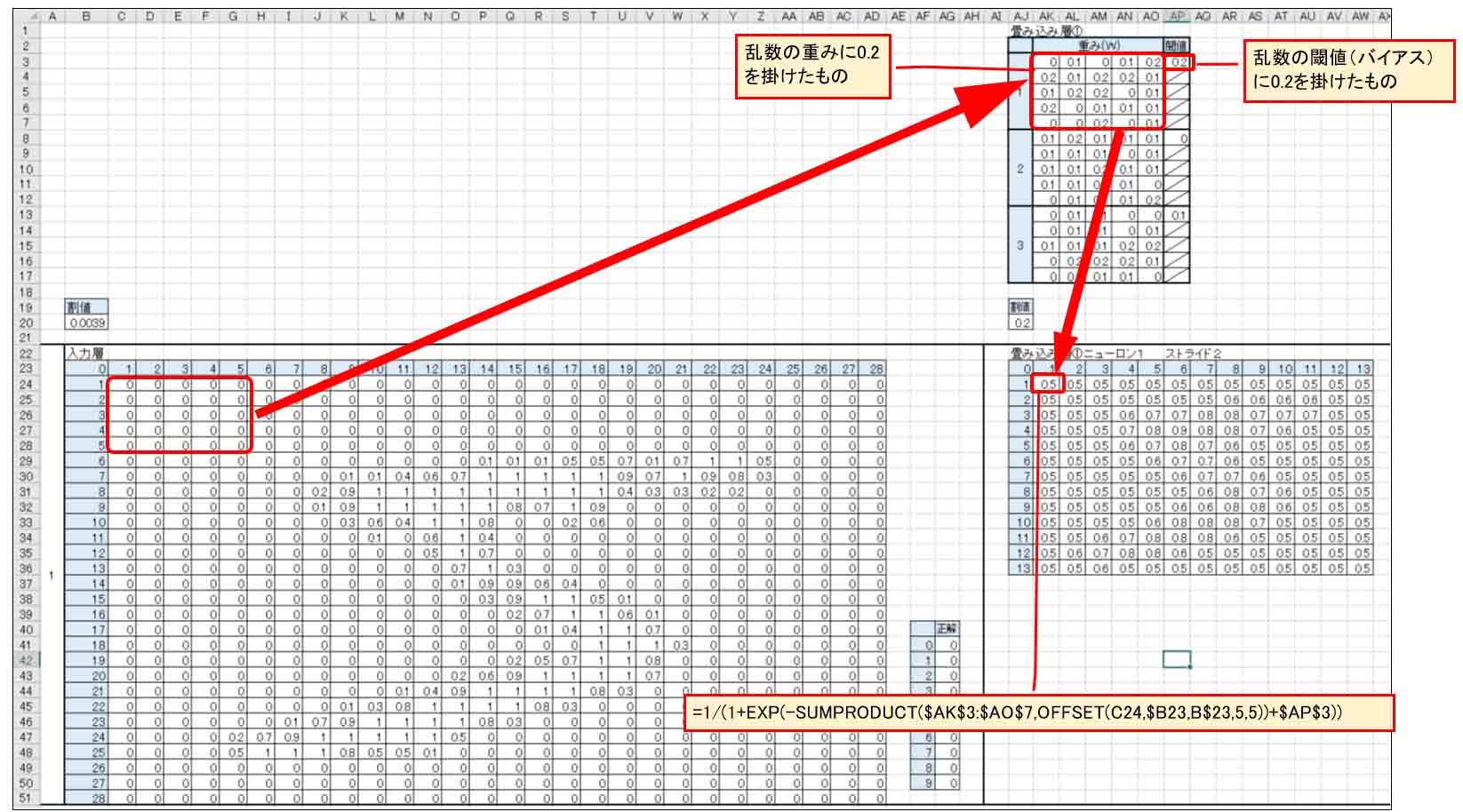
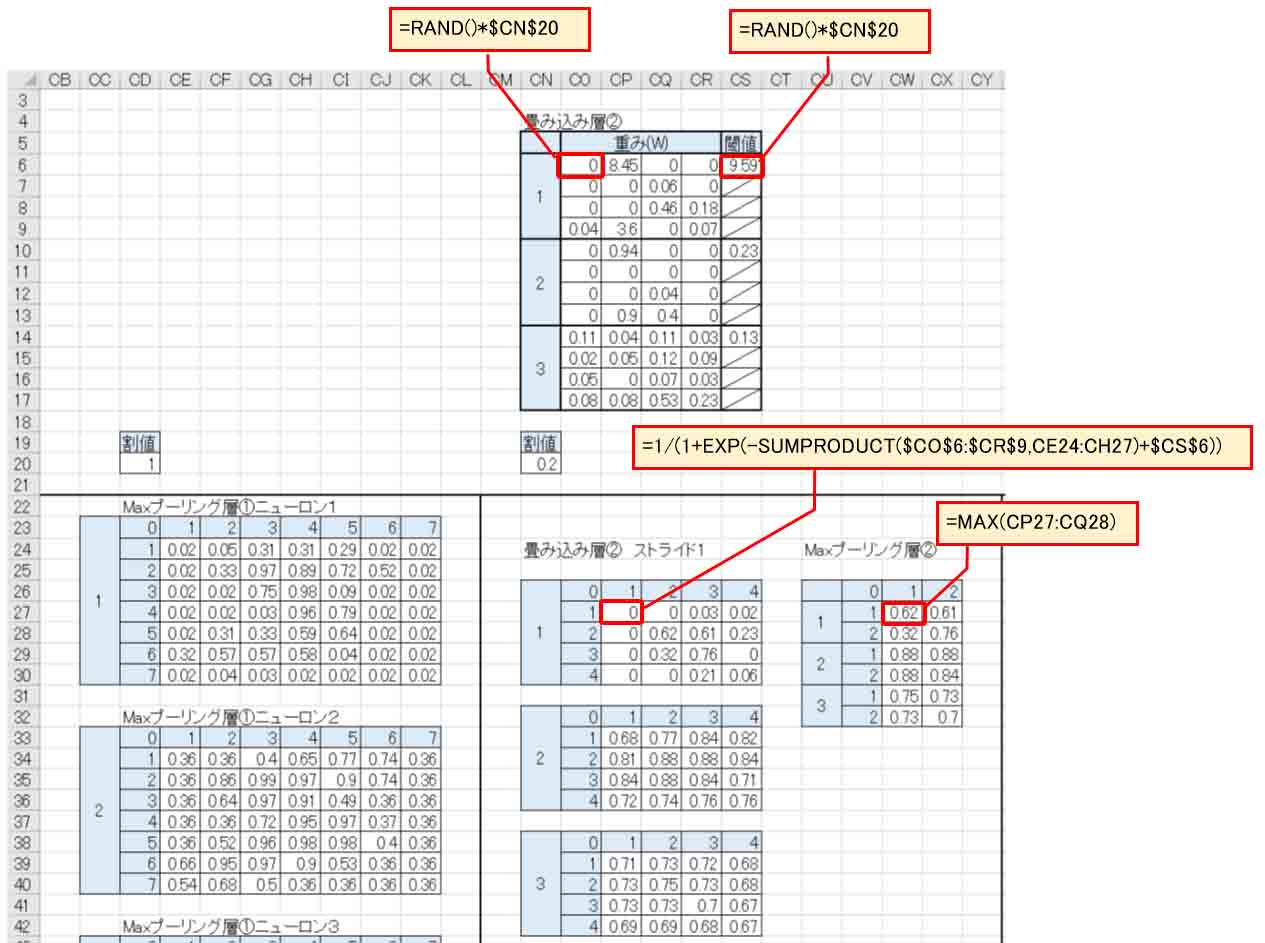
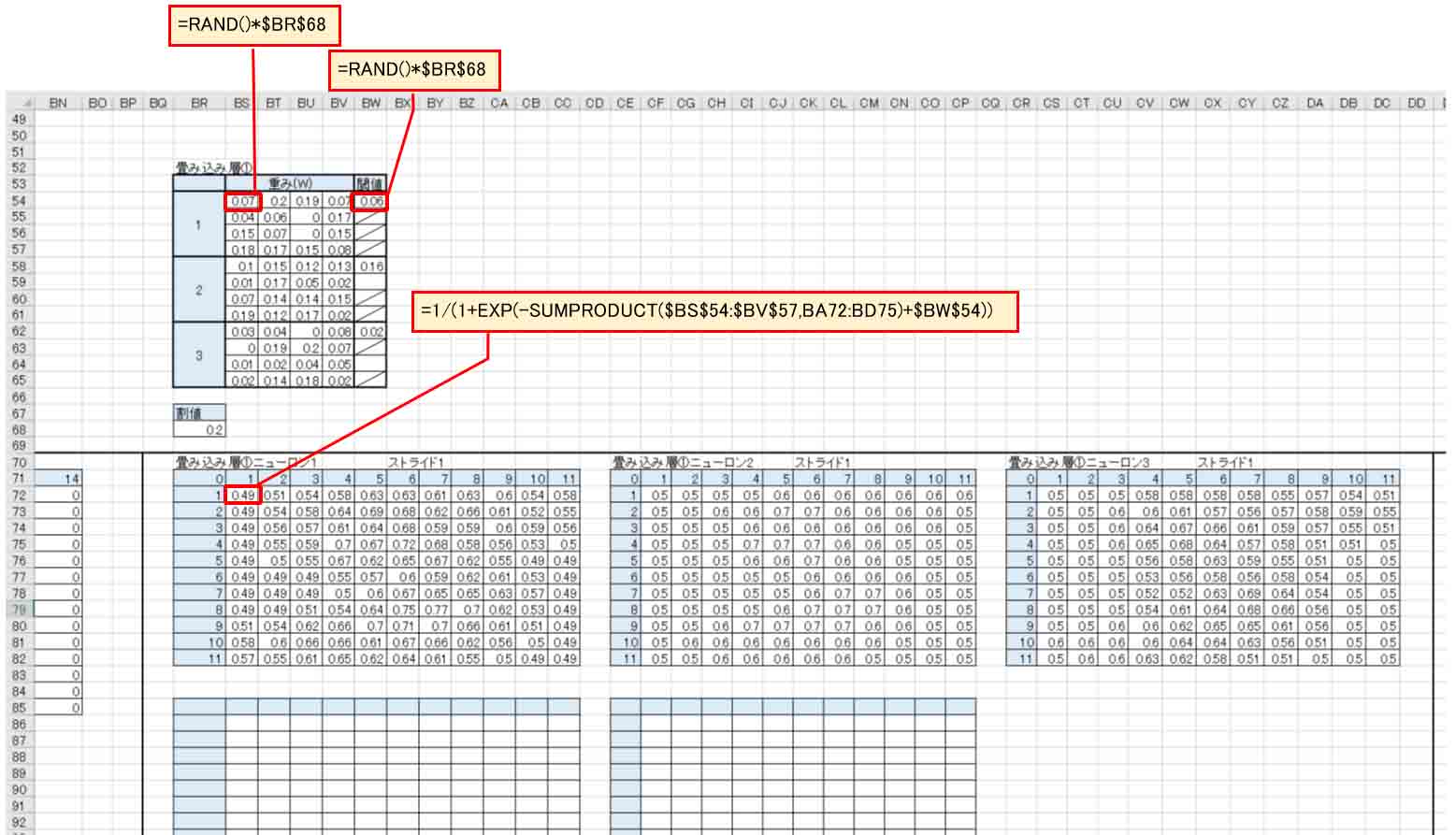
まず、畳み込み層の重み(W)として5×5の乱数を作り、それを3組、つまりニューロン(ノード)を3つ作ります。
因みに、ニューロンのことをノードと表現することもあるそうです。
そして、前回記事のように閾値(バイアス)を乱数で作ります。
下図のようになります。
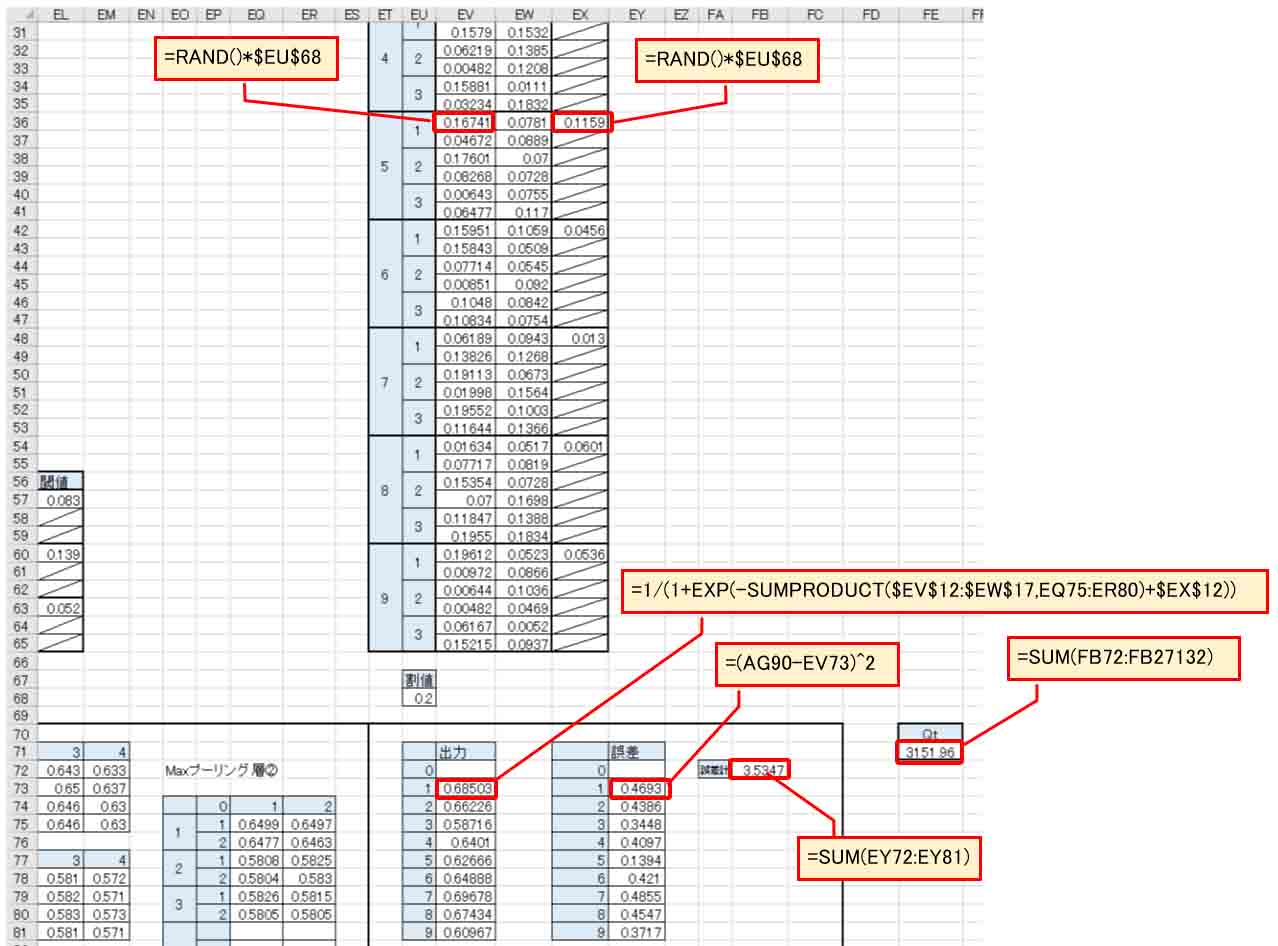
そして、入力層の左上端の5×5マスと重み(W)をSUMPRODUCT関数で掛け合わせ、バイアスを加味したシグモイド関数で出力するようにします。
因みに、重みとバイアスの乱数には全て0.2を掛けておきます。
これは書籍「Excelでわかるディープラーニング超入門」に習いました。
(図02-02)
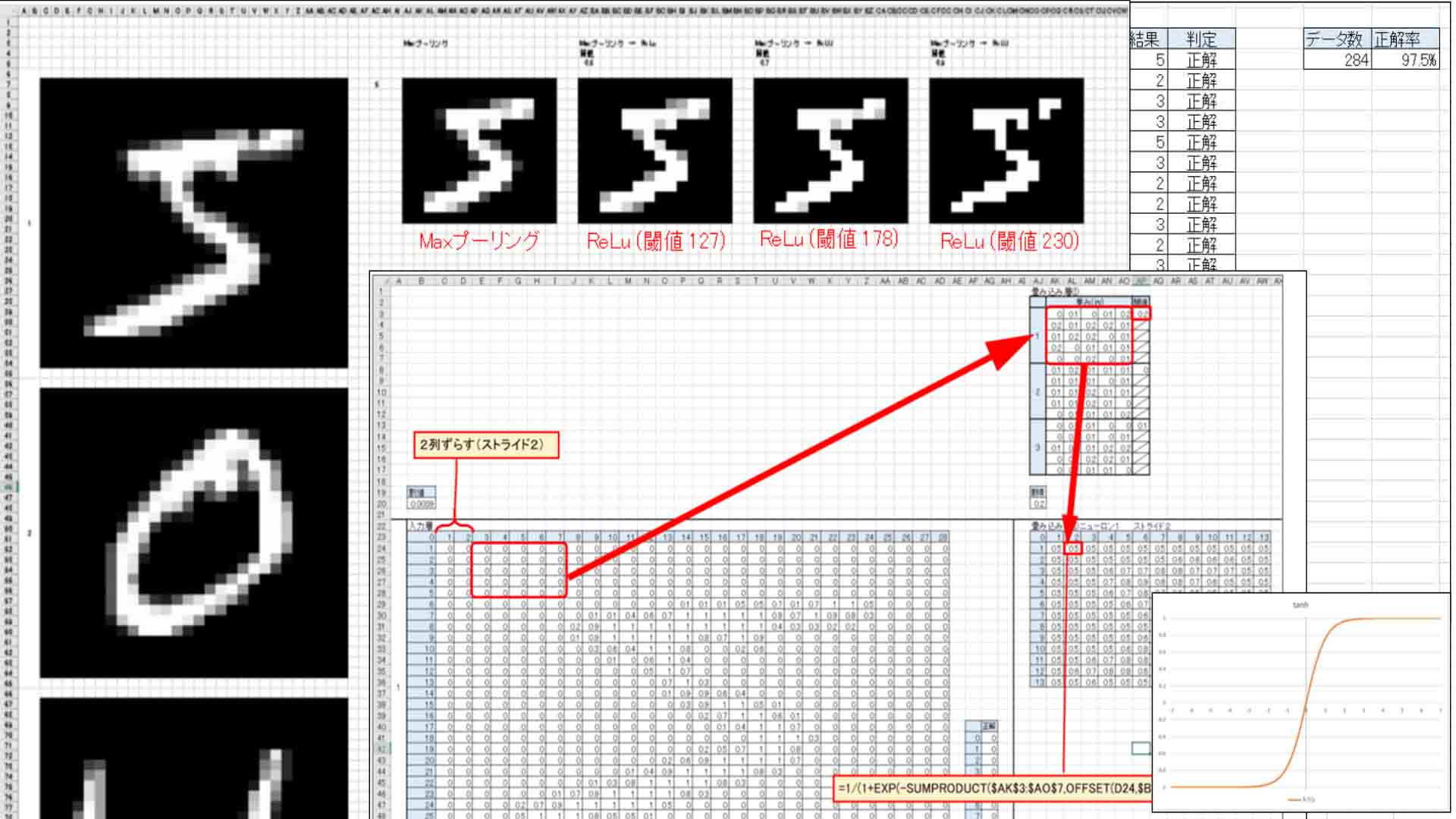
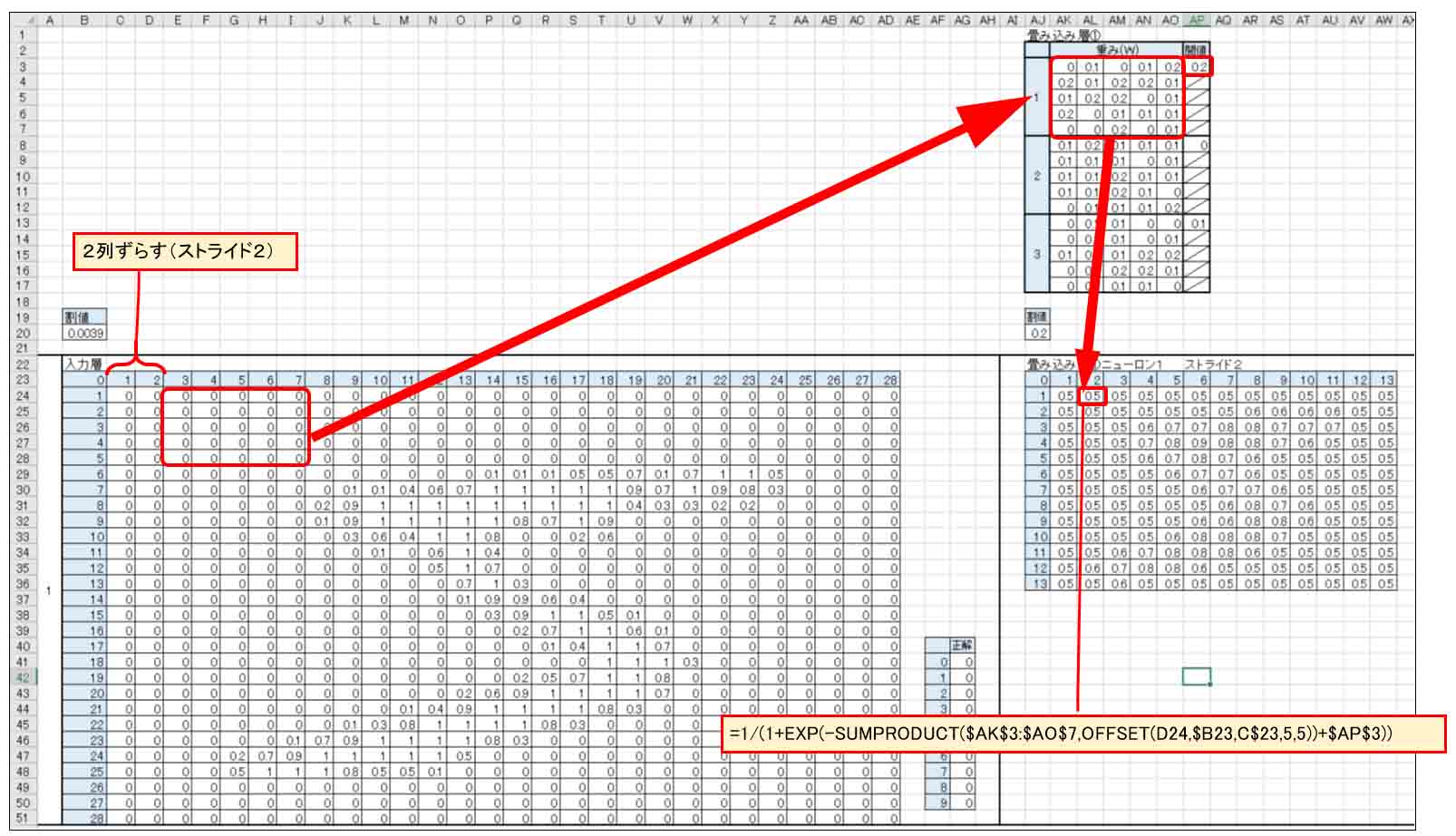
次に下図の様に入力層の5×5のマスを2列分ずらして、重みと閾値(バイアス)を掛けてシグモイド関数出力します。
(図02-03)
書籍「Excelでわかるディープラーニング超入門」では、1列ずつズラしていますが、ここでは畳み込み層の欄を小さくするために2列ずらしました。
この「ズラし」を専門用語で「ストライド」と言うらしいです。
この場合はストライドが2ということになります。
これを繰り返していきます。
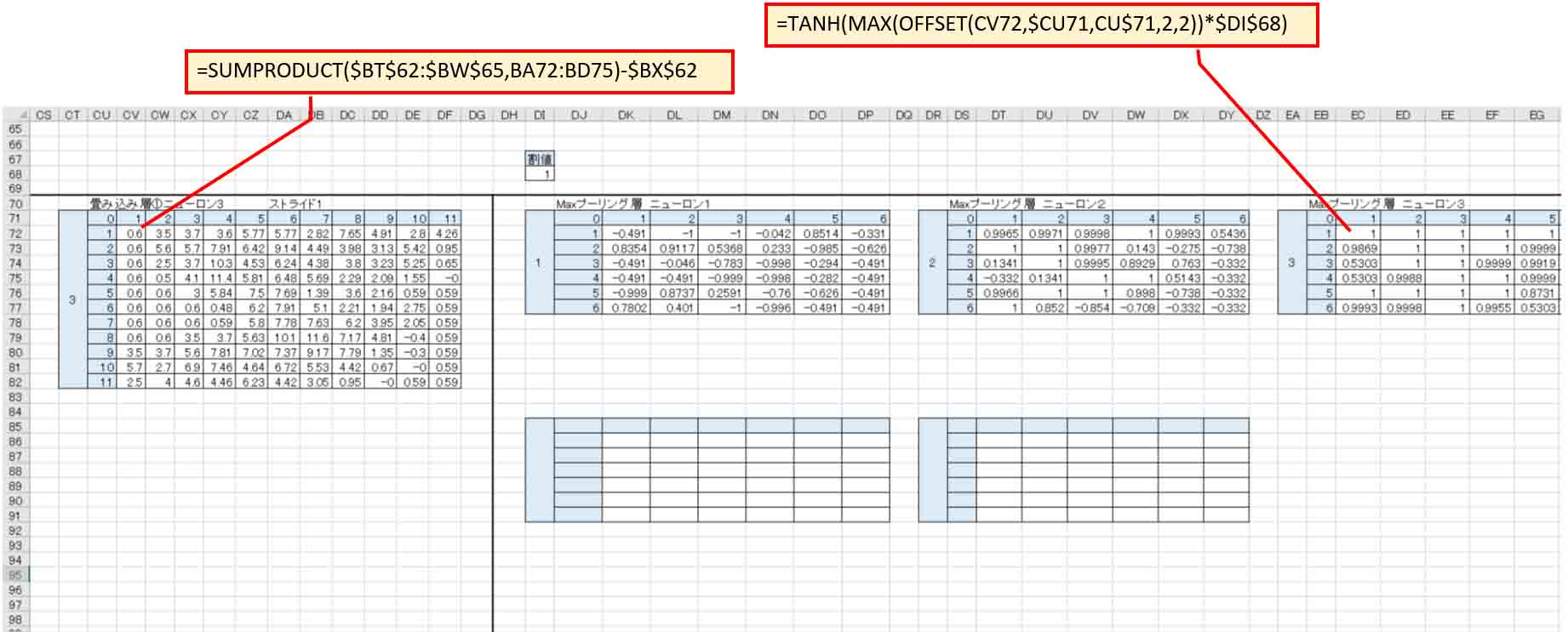
それで、畳み込み層①のニューロン1では、28×28マスが13×13というマスに縮小できました。
もし、ストライド1だったとすると、24×24となってしまい、まだまだ大きすぎます。
ストライド2の方が効率的ですね。
ただ、ストライド2は1よりも学習精度が悪くなります。これは後々分かってきますが、頭に入れておかないといけません。
(この重み(W)による畳み込みの意味は後の3章で述べています。)
ところで、ストライド2ということは、Excelでは2つおきにセルを参照して表を作らねばなりませんが、それってセル参照が難しいと思いませんか?
いちいち1つずつセルに入力していけば良いかもしれませんが、せっかくExcelを使っているのにそれでは面倒過ぎます。
実は、私は随分前からその方法を探していて、結局分からずに今日まで放置していたのですが、最近ようやく方法が分かりました。
OFFSET関数を使えば良いのです。
背景が青色セルの見出し番号を参照して使うところがミソです。
これは便利ですよ~!
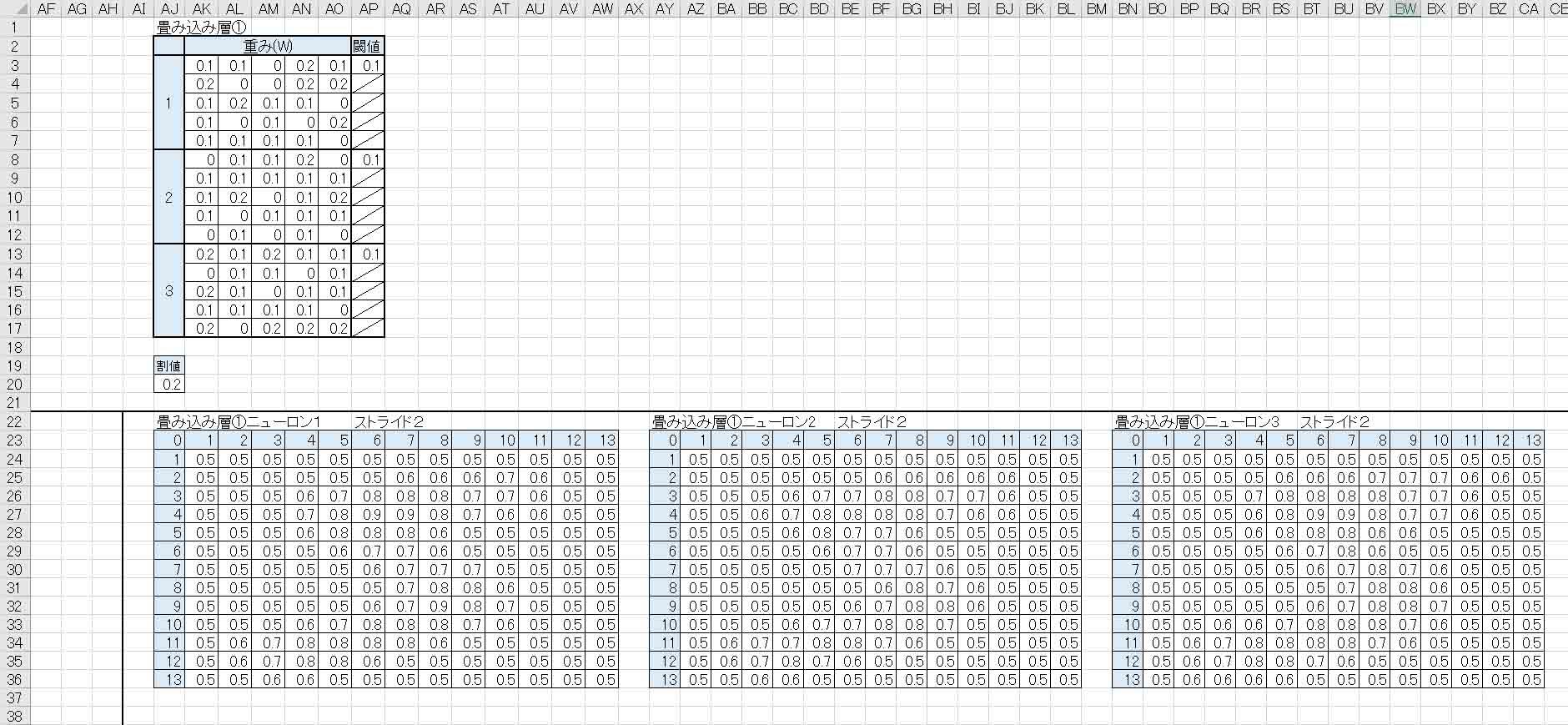
そんな感じであと2つのニューロンも同じように作ります。
畳み込み層①のニューロンは3つまでとします。
それ以上になると、Excelのソルバーではパラメータが多すぎて計算できません。
ソルバーは200個までのパラメータしか変更できないからです。
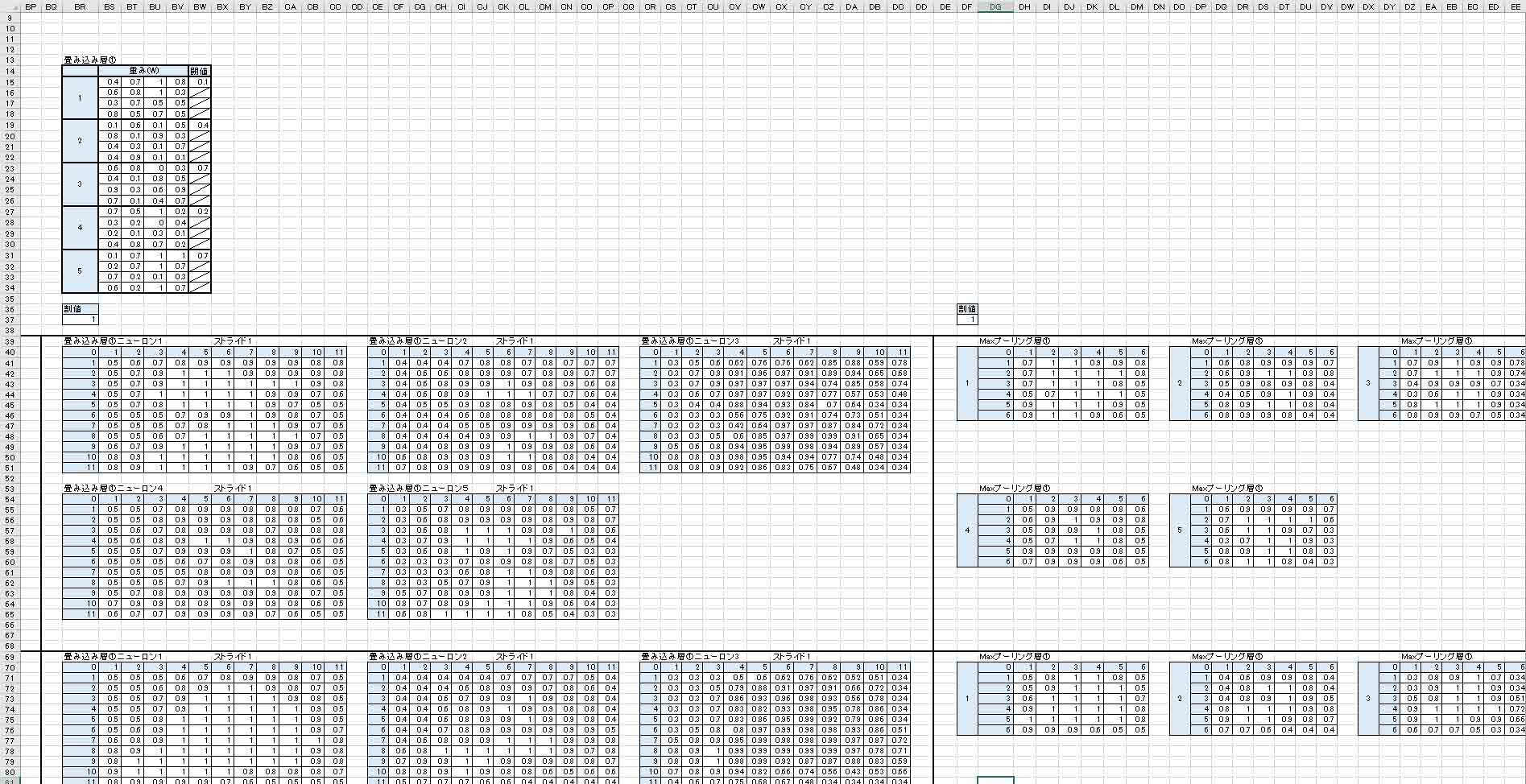
畳み込み層①は、下図の様になります。
(図02-04)
本当は縦にニューロンを並べたかったのですが、表示の都合上横並べにしました。
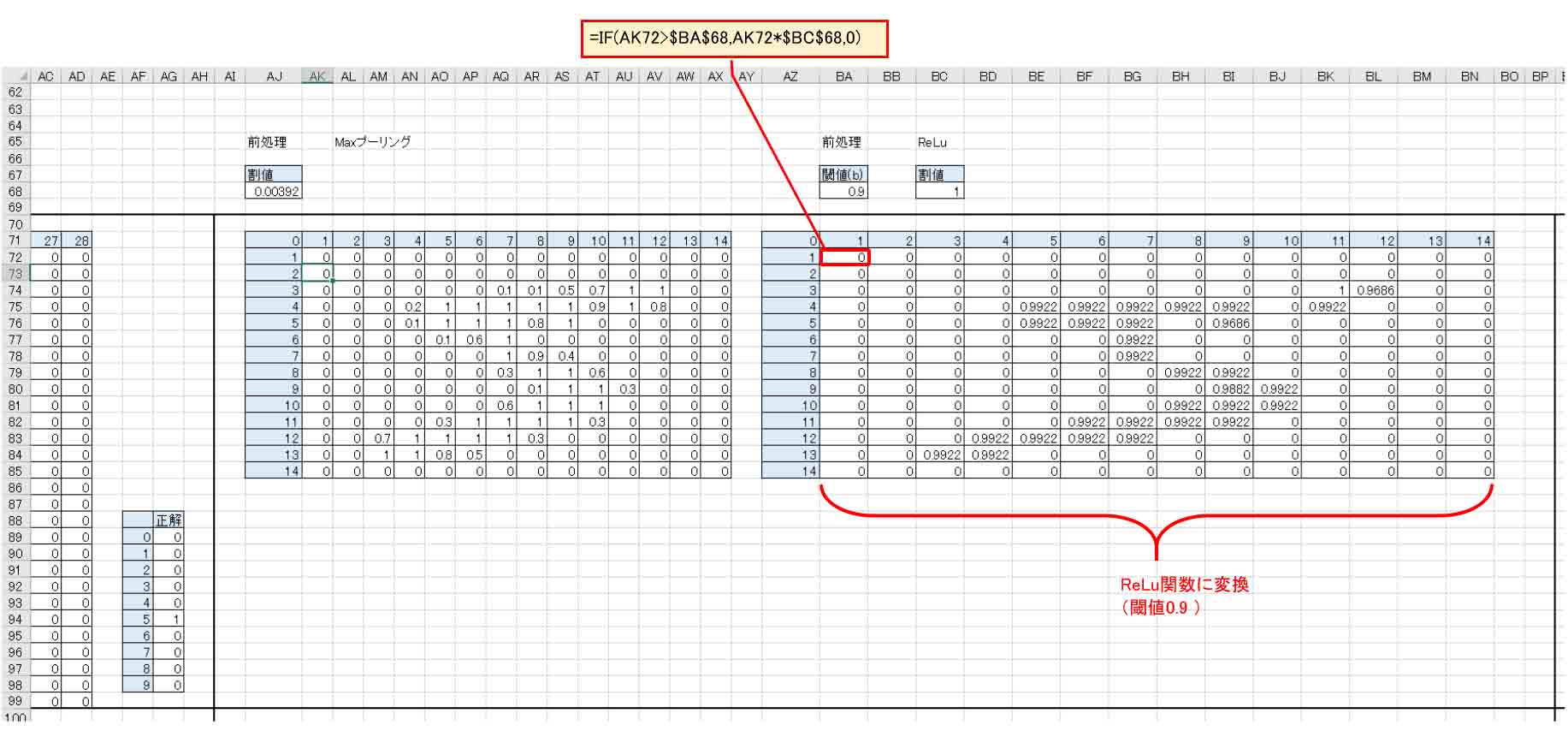
2-2. MAXプーリング層を作る
続いて、書籍「Excelでわかるディープラーニング超入門」に習って、各々の畳み込み層ニューロンからMAXプーリング層を作っていきます。
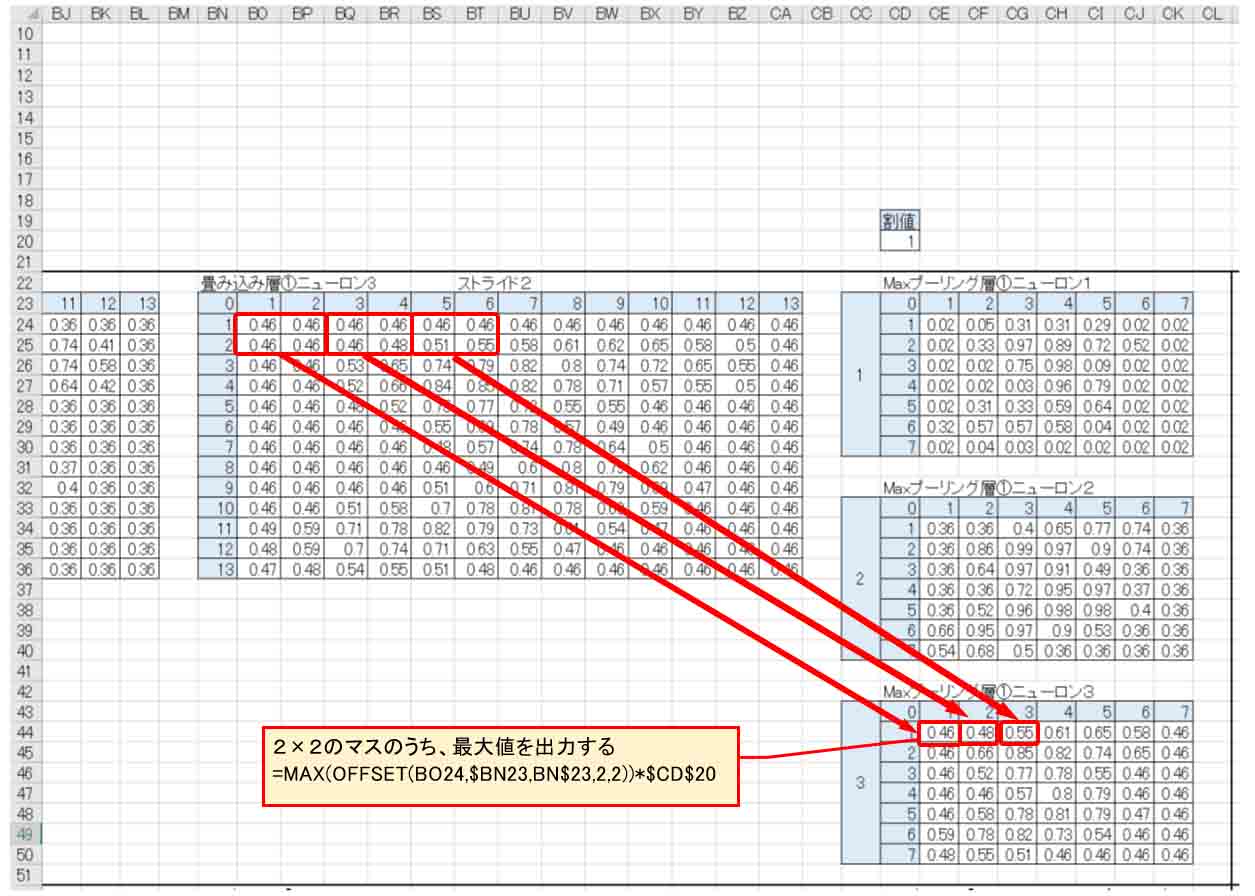
2×2のマスごとにその中の最大値を出力します。
以下の様な感じです。
この図では表示の都合上、3番目のニューロンを見ています。
(図02-05)
これは畳み込み層(Convolution)とは異なり、重み(W)やバイアス(b)は無く、2×2のマス目もダブらせずに抽出していきます。
図のように単純に2×2マスごとに分けて、その中の最大値を出力させただけです。
これもセル位置を1つ飛ばして参照させるので、先ほどと同じようにOFFSET関数を使いました。
上にある割値は、重みとバイアスに掛けていたものと同じ目的のものです。
ソルバー計算の時に速く収束するようにいろいろ割値を変えて学習させていくためのものです。
今回は1としました。
このMAXプーリング層を作ると、13×13マスが7×7マスになり、1つのニューロンに対して出力が49にまで縮小できました。
それでもまだ多すぎるので、もっと凝縮せねばなりません。
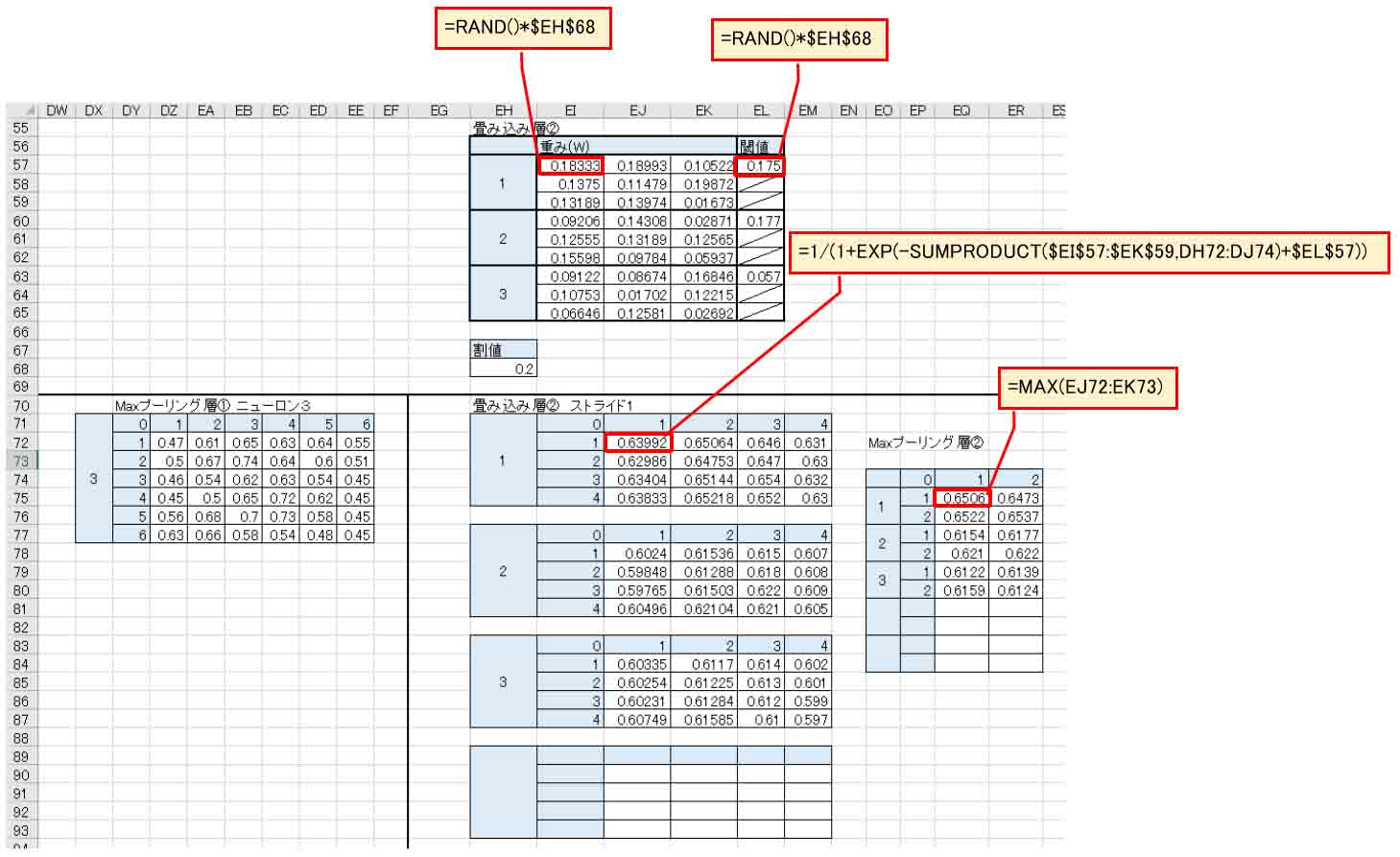
2-3. 2つ目の畳み込み層とMAXプーリング層を作る
では、ここからは最初に紹介した書籍「Excelでわかるディープラーニング超入門」には無いことをやってみます。
更に2つ目の畳み込み層②を作って圧縮させてみます。
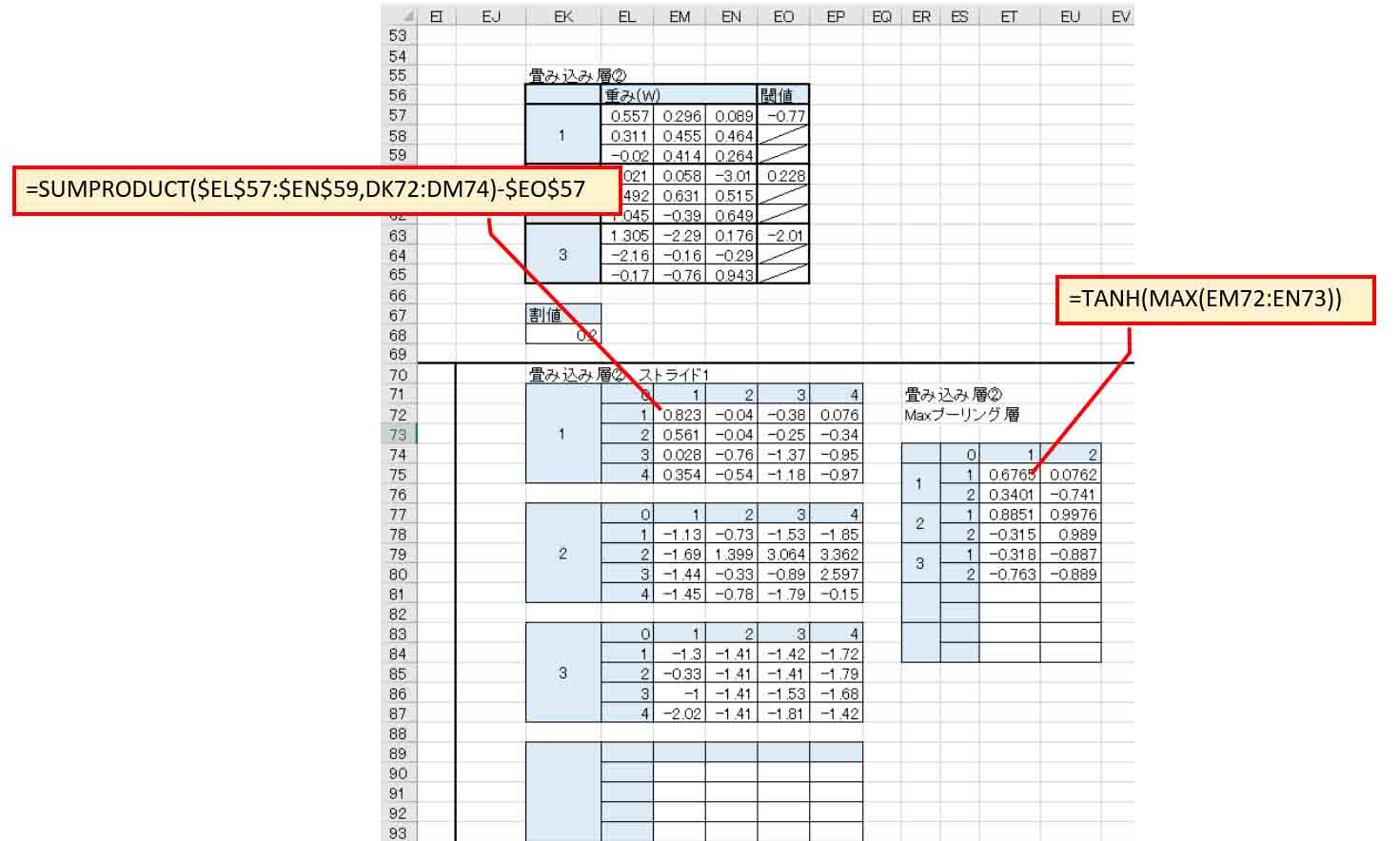
畳み込み層①では5×5マスで畳み込んでいましたが、今度は4×4マスとし、重みとバイアスに乱数を設定します。
乱数には先ほどと同じように0.2を掛けておきます。
そして、下図の様に畳み込み層②のストライドは1とします。
そうすると、OFFSET関数が不要になるので簡単ですね。
これでニューロン一つの出力は4×4マスとなり、16個まで凝縮できました。
そして、先と同じようにMAXプーリング層②も作ります。
2×2のマスでプーリングしていきます。
(図02-06)
すると、MAXプーリング層②の出力は1ニューロンあたり4個にまで凝縮できました。
ニューロンの総数は3なので、出力の総数は12個にまでできました。
こうなると、次に作る出力層の計算はだいぶ楽になります。
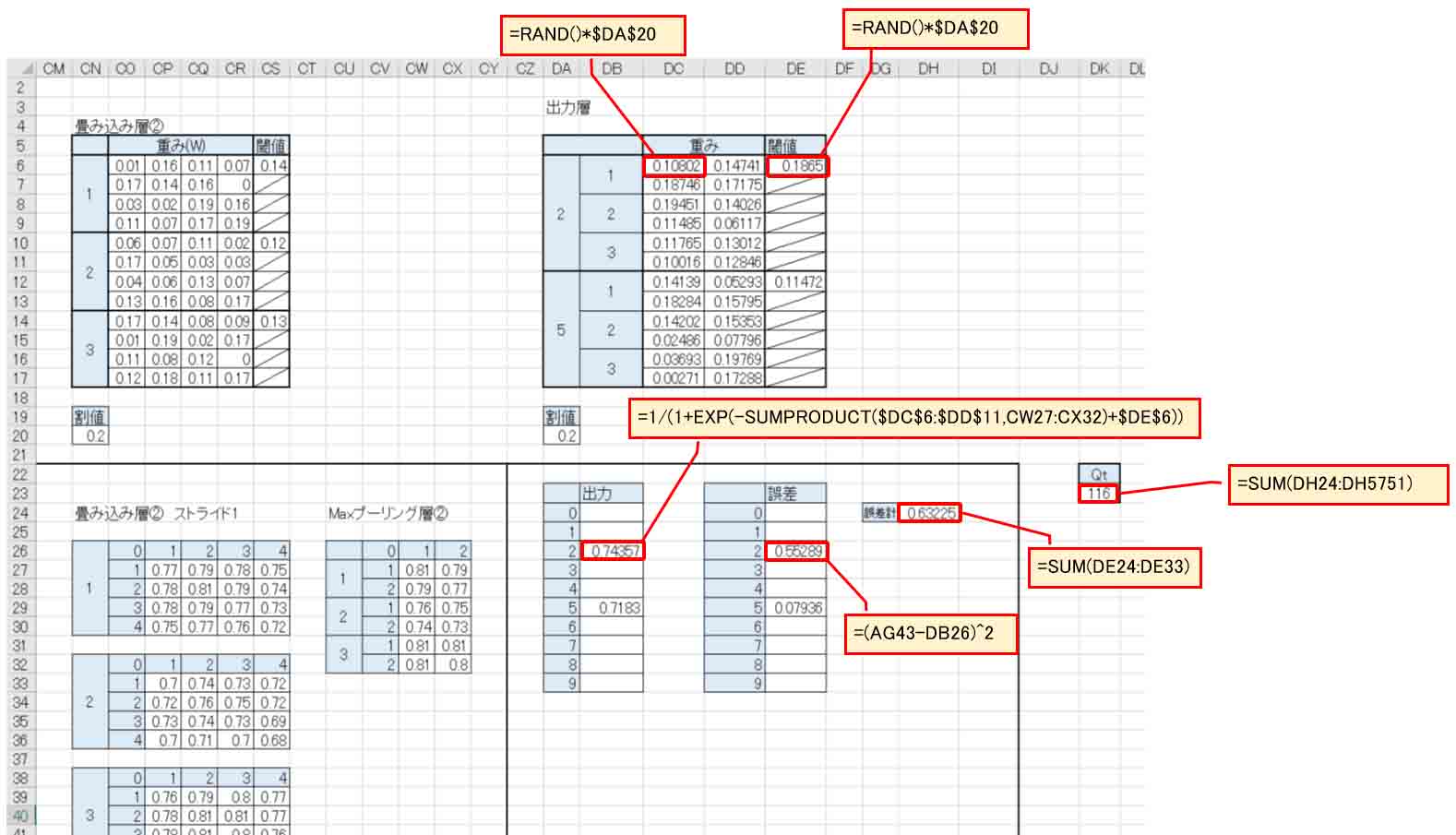
2-4. 全結合(affine)して出力層を作る
では、今度は出力層を作っていきます。
最初に紹介した書籍「Excelでわかるディープラーニング超入門」に習って、先に作ったMaxプーリング層②の出力を全結合して出力層を作ります。
全結合とは affine と言うらしいです。
要するに、Maxプーリング層の出力すべてのニューロン(ノード)に対して、重み(W)とバイアス(b)を全て結合させていくわけです。
難しく見えますが、要は畳み込み層を作る時と同じように、SUMPRODUCT関数を使って掛け合わせているだけです。
ただ、何度も言っているように、Excelのソルバーの制約上、200個までのパラメータしか対応できませんので、出力層のニューロン数については気を付ける必要があります。
今まで作ってきたパラメータ数を計算してみると、
畳み込み層①: 重み 5×5×3 = 75個
バイアス 3個
畳み込み層②: 重み 4×4×3 = 48個
バイアス 3個
合計: 75 + 3 + 48 + 3 = 129個
となります。
ということは、残り71個までのパラメータしか扱えません。
すると、Maxプーリング層②の出力数は12個なので、出力層ニューロン1つについて12個の重みと1個のバイアスが必要です。
つまり、71の中に13が5つ入るので、出力層のニューロン(ノード)数は5つまで可能ということになります。
ただ、今回はいろいろ実験して精度が出なかった(実はソフトマックス関数を使ってなかったのが原因と後で分かった)ので、まずは出力層のニューロン(ノード)を2つで実験してみました。
こんな感じです。
(図02-07)
数値が2と判定を期待するニューロン(ノード)には、12個の重みと1個のバイアスを作ります。
同じように、5と判定を期待するニューロンにも重みとバイアスを作ります。
それぞれ先と同じように割値を0.2としておきます。
出力は参考書に習って今までと同じようにシグモイド関数にしておきます。
誤差(平方誤差)は前回記事で述べたように、正解値を1として差し引いて2乗したものです。
誤差計は各ニューロンの平方誤差を合計したものです。
そして、Qtは前回記事と同様、各学習データの誤差計全てを合計したものです。
このQtが最小になるように重みとバイアスの数値を変化させる学習計算をすれば良いわけです。
2-5. ソルバー計算で学習させた結果
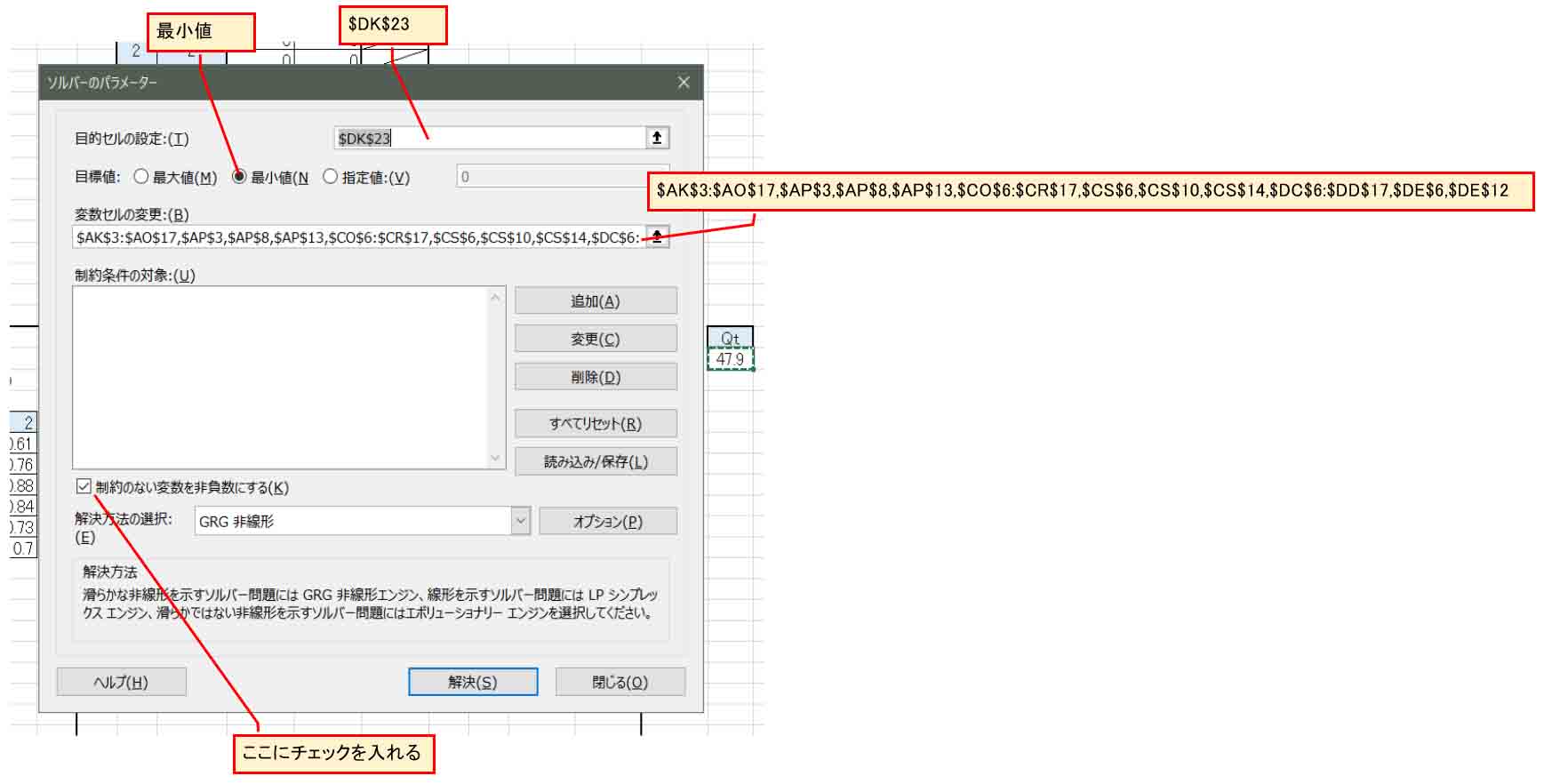
では、とりあえず前回記事と同じようにソルバー計算させてみます。
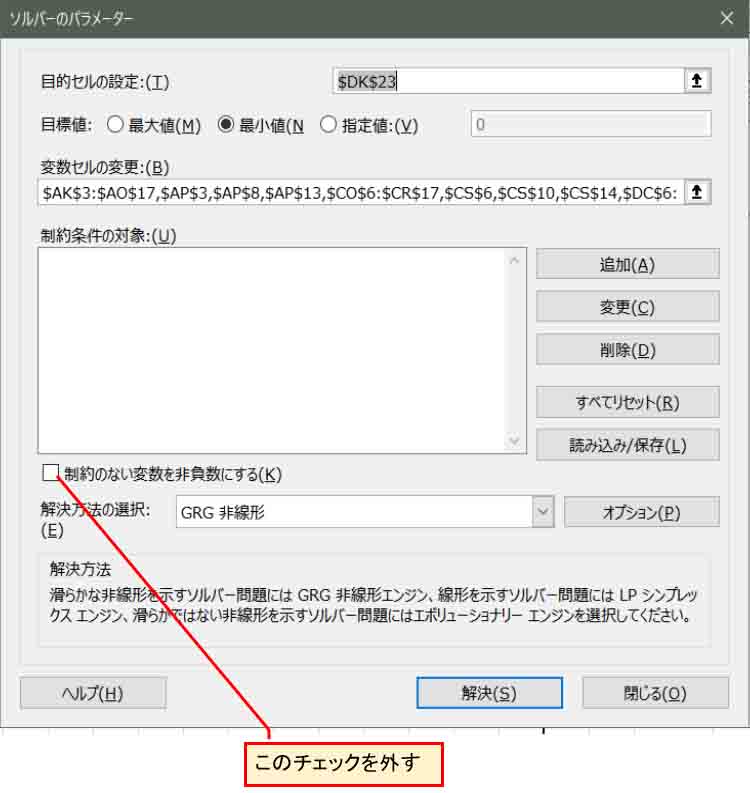
下図の様にまずは「制約のない変数を非負数にする」というところのチェックを入れて、正の数になるように計算さてみます。
「変数セルの変更」欄は
$AK$3:$AO$17,$AP$3,$AP$8,$AP$13,$CO$6:$CR$17,$CS$6,$CS$10,$CS$14,$DC$6:$DD$17,$DE$6,$DE$12
という感じです。
(図02-08)
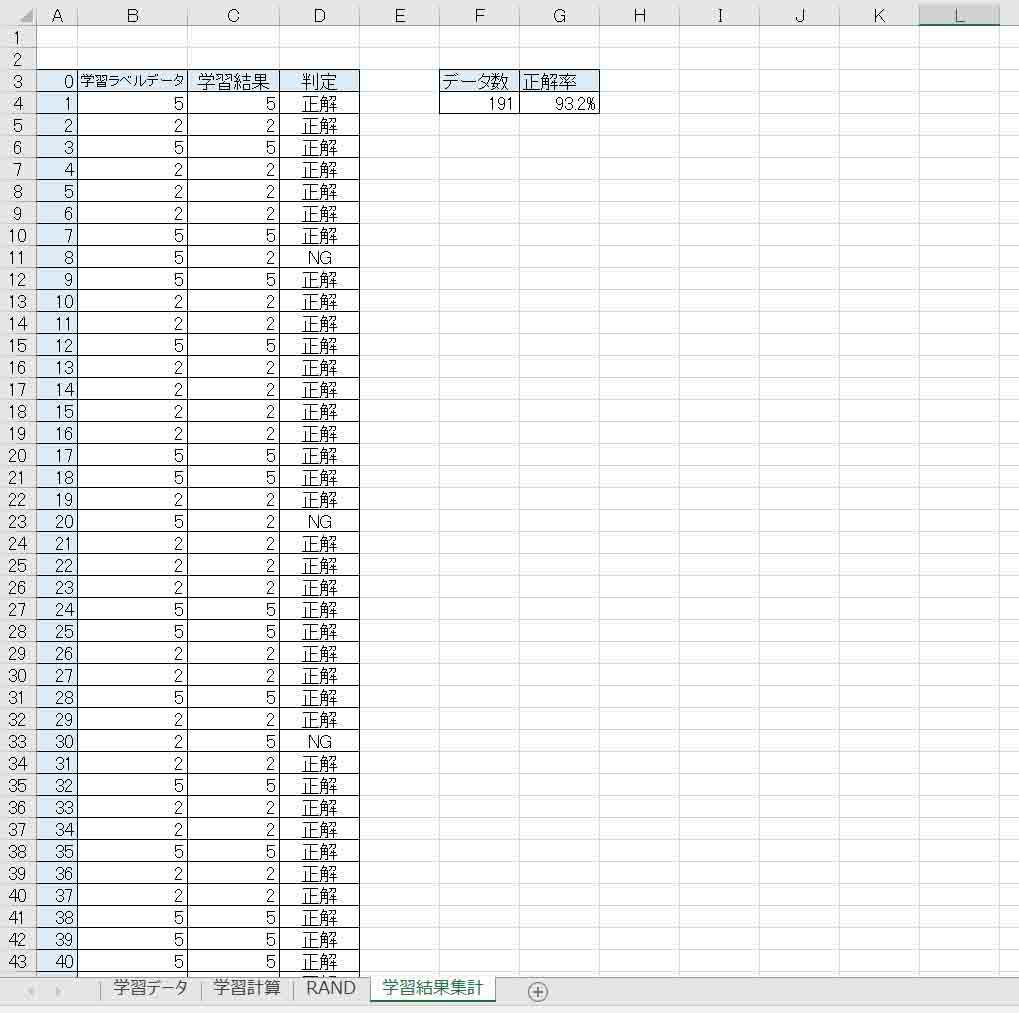
結果、Qtの値が116から47に収束しました。
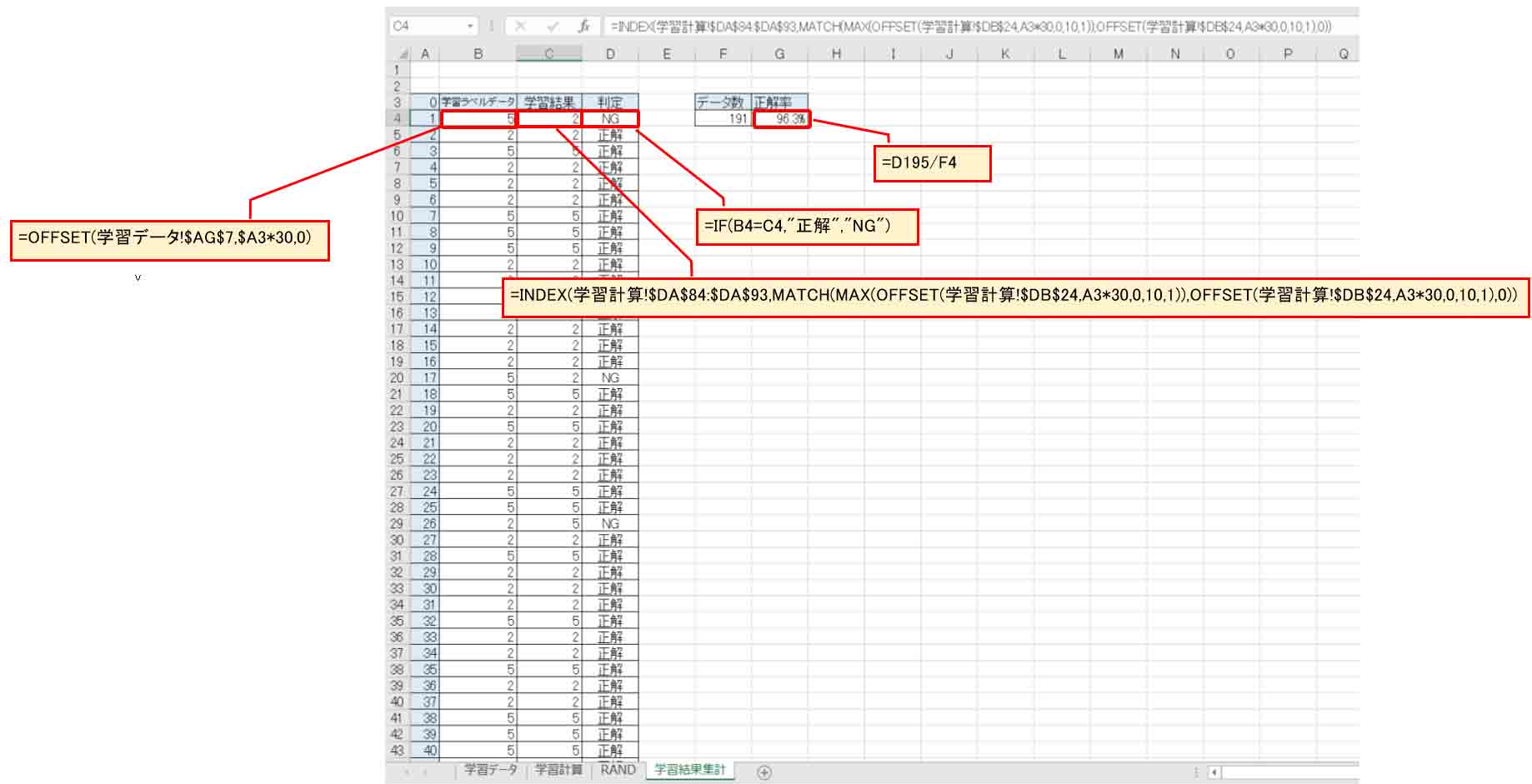
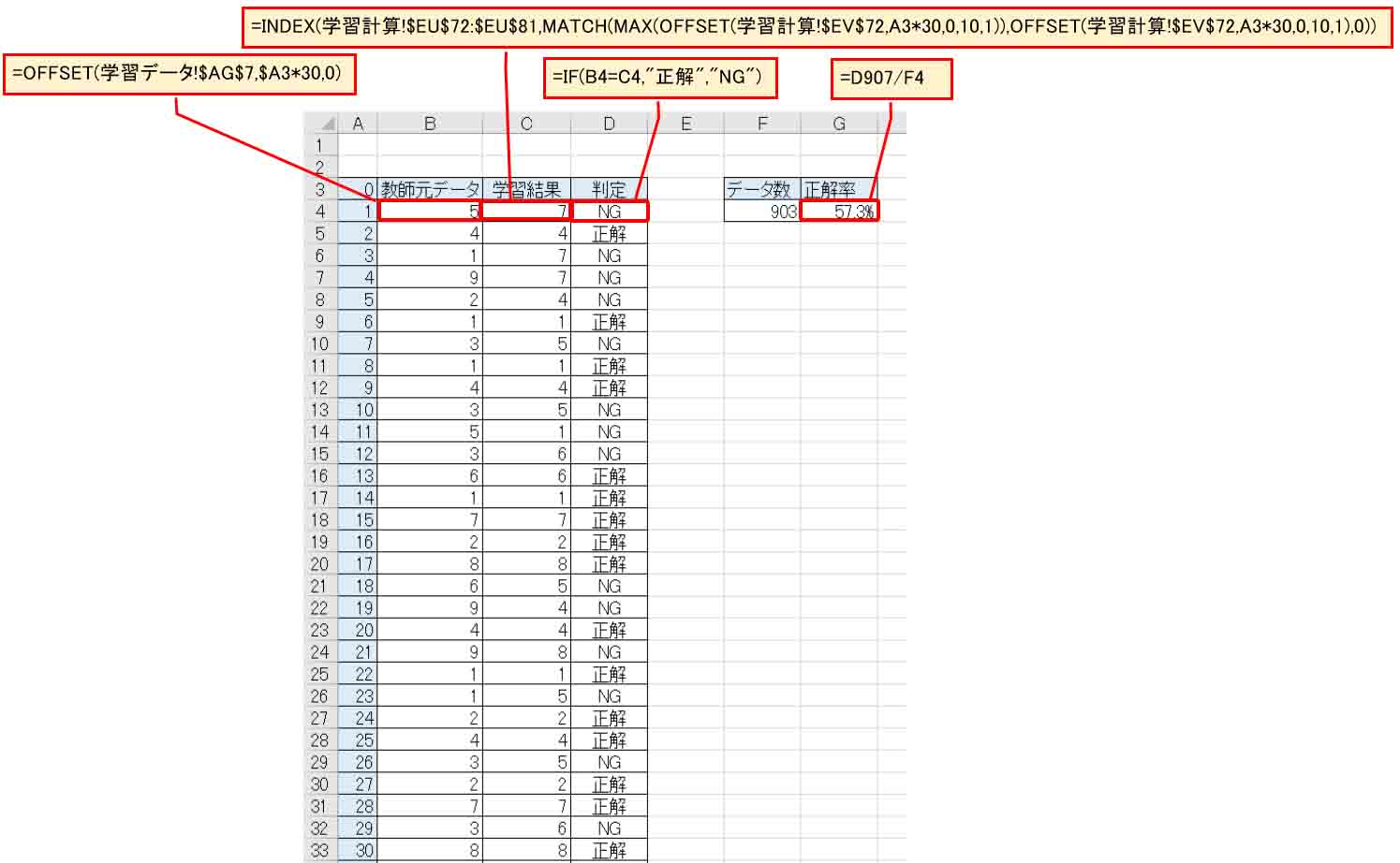
新たに「学習結果集計」というシートを作り、下図の様に一覧表示させてみました。
(図02-09)
INDEX関数やMATCH関数などを使っています。
結果、191データ中、正解率が96.3% となりました。
なかなか良いですね。
98%以上が目標なので、あともうちょっとです。
一覧をざっと見ると、まだまだNGが多い感じがするので、あまり精度が上がっていないように見受けられました。
2-6. 重みとバイアスに負の値を許容してみる
先のソルバー計算の重みとバイアスは、正の値のみしか許容していませんでした。
ならば、前回記事で良い結果が得られたことを受けて、ソルバー計算で負の値を許容してみます。
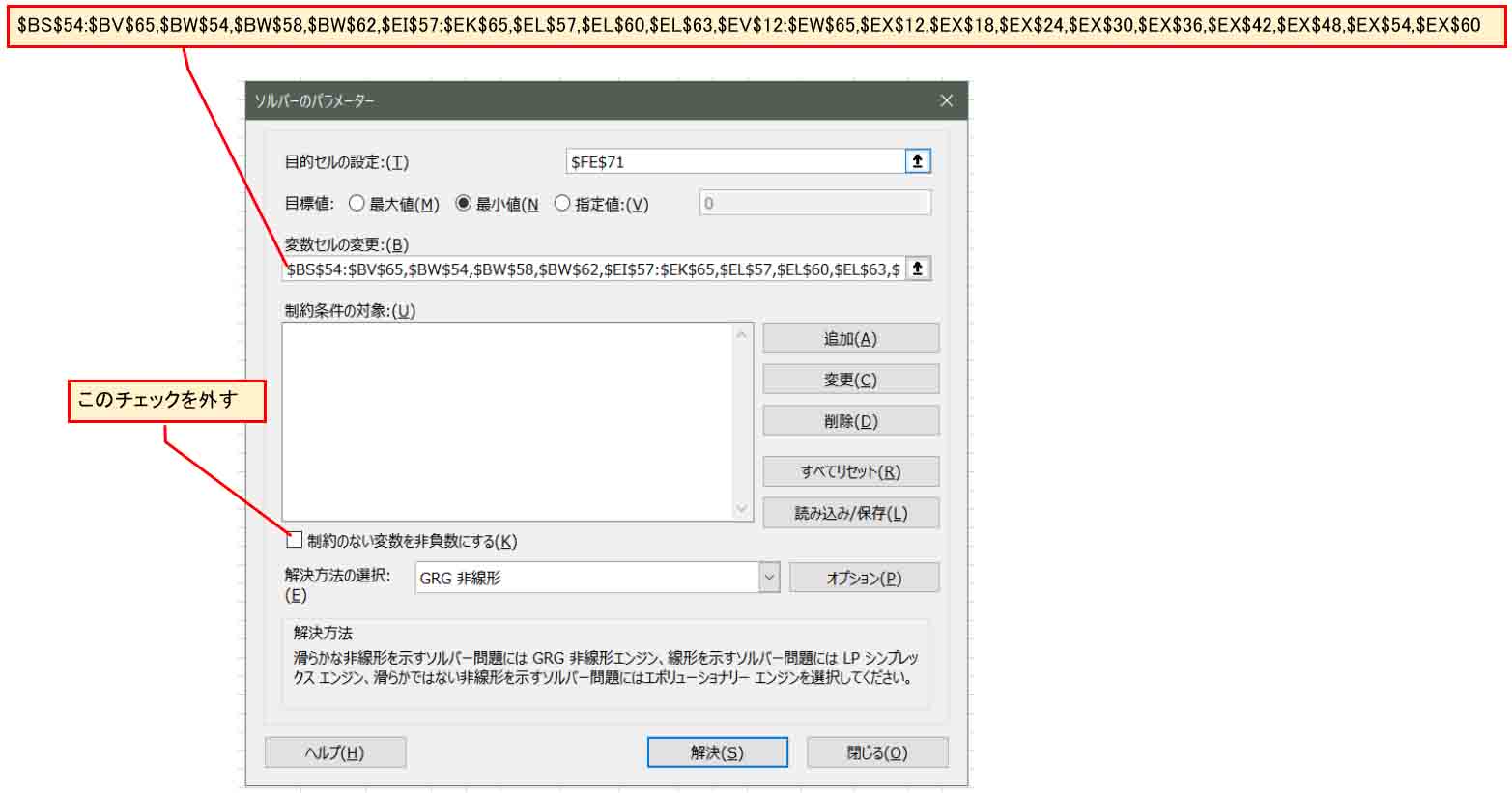
重みとバイアス全てに乱数と割値を入力し直して、下図の様にソルバーを起動し、「制約のない変数を非負数にする」のチェックを外します。
(図02-10)
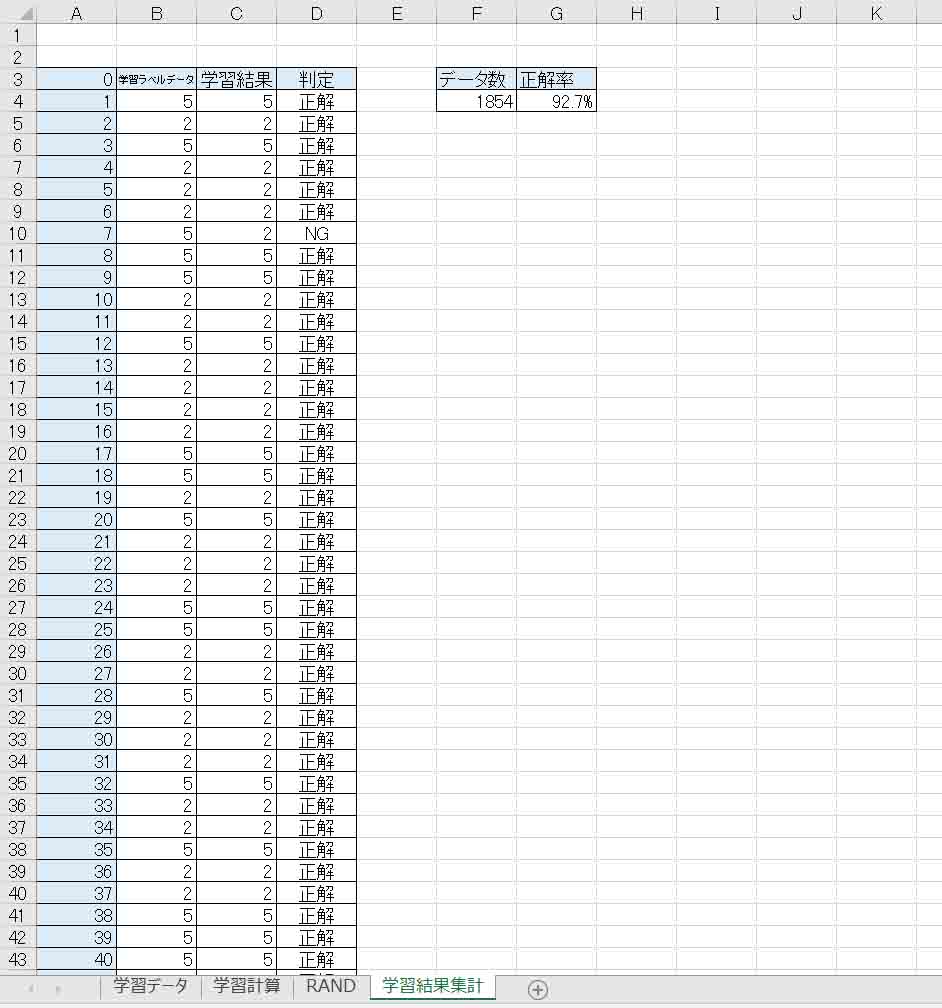
これで、計算すると、私のパソコン環境で1時間30分くらいかかり、Qtの値が22.9まで収束しました。
結果は以下の感じです。
(図02-11)
正解率は 93.2% でした。
おやおや?
前回記事の流れでは、負の値を許容した方が結果は良くなるはずなのに、今回は逆に悪くなりました。
Qtの値が小さくなったにもかかわらずです。
もしかして、ソルバー計算が極小解で止まってしまったのかも知れません。
ちょっとこれは納得いかないですね。
疑問が出てきたので、これからあれこれと試行錯誤して実験していきます。
3.学習後の重みと畳み込み演算の不思議
さて、ここで先の学習で得られた畳み込み層①の重み(W)について重点的に考えてみたいと思います。
重みは何を意味しているのか数値だけでは良くわからないので、下図のように視覚化しやすいように0~255の値になるように変換しています。
そして、マクロ(VBA)でセルに色を付けて表示させてみました。
(図03-01)
これを見ても、重みは何を表しているのかサッパリ分かりません。
では、重みの役割を分かり易くするため、別途新たにExcelファイルを作って、14×14 pixel で4の数字画像を使って、独自に重みを付けて畳み込み演算させてみます。
そして、下図の様に視覚化してみました。
(図03-02)
これは私が勝手に4という手書き文字の特徴を切り出して、それに重み付けをしています。
手書き線が交差するところは、他にも8という数字が考えられますが、この5×5の切り出した画像を見る限り、多くの人間は4と判断するだろうと思います。
白い部分を重み0.3とし、他は0と設定しました。
重みは「フィルター」とも呼ばれているようですので、畳み込み演算というのは、5×5 pixel のこの画像フィルターで14×14 pixelの画像をスキャンして一致するところ、もしくは近い特徴のところが数値が大きくなると想像すると分かり易いかと思います。
スキャンする移動距離は1画素、つまりストライドは1です。
畳み込み層をイメージ化した白黒画像は、マクロ(VBA)で作りました。
イメージ化したものをジーッとよく見ると、重み(フィルター)と一致したところは一段と明るい白色になっていて、その重み(フィルター)パターンから遠ざかるにしたがって暗い色になっていることが分かります。
つまり、画像の中央付近の一点が最も白く明るいことが分かります。
「その明るい色の付近に正解があるよ!」という感じで語りかけているように見えます。
視覚化すると一発で分かりますね。
Maxプーリングの画像を見てみると、畳み込み層の縮小版のような感じですね。
画像を圧縮しても、重み(フィルター)パターンとマッチしたところが変わらずに継承されて表示されていることが分かります。
ところで、このMaxプーリングというのを畳み込み画像と見比べると、畳み込み画像を圧縮したように見えますね。
もしかしたら、画像圧縮に使えそうな気がします。
これについては5章で述べます。
では今度は、手書き線の交差するところが一切無い1という数字の画像にこの重み(フィルター)パターンを適用してみます。
すると下図のようになりました。
(図03-03)
これを見て分かる通り、先ほどの数字4と比べて、ひと際明るい画素が無いですね。
全体的にボヤけた感じです。
ということは、重み(フィルター)にマッチしたところが無いということです。
こうやって、数値をセルの背景色で表現すると一目瞭然で、重みと畳み込み演算の役割が良くわかりますね。
フィルターを通したレンズで画像を見て、1という数字がボヤけているようなイメージですね。
このことから、「重み」という数値は、特徴パターンを切り出したフィルターという意味が良くわかりますね。
そして、畳み込み演算は、そのフィルターパターンに一致、もしくは近いものであれば高い数値になって現れてくるということも良くわかります。
それから考えると、出力層が多くて判定する要素が多い場合、この重みパターンが多数無いと正常に判定できそうもないということが想像できますね。
SonyのYouTube動画のDeep Learning入門で述べられているように、畳み込み層の最初のニューロンは最も多くした方が良いという意味がよく分かりました。
そして、ストライドは1が最も精度が良く、ストライドが大きくなるにつれて重みパターンと一致する確率が少なくなるので、当然精度は悪くなることも分かりました。
ところが、(図03-01)の重みパターンを視覚化したものを改めて見直してみてください。
すると、2と5という数字の特徴パターンが見て取れません。
というか、人間の私には見て取れませんと言う方が正解なのかもしれません。
どこを切り取ったパターンなのかさっぱり分かりません。
それなのに、96%の正解率を叩き出すことが何とも不思議です。
これがディープラーニングという物の妙なのかも知れません。
重み付けは人間が独断でやってはいけない、ということなのかも知れませんね。
なお、この章で紹介したExcelファイルはGiHubに上げていません。
4.学習データを約10倍増やしてみる
さて、2章ではなかなか良い学習結果が得られましたが、まだイマイチな結果だったので、前回記事の教訓から、学習データを極端に増やせば、もしかしたら正解率を上げられるかも知れないと考えました。
そこで、先ほどはMNISTの1000データの中から2と5の数値を抽出していましたが、今度は10倍の10000データの中から2と5の数値を抽出してみます。
これは計算にとても長い時間を要しました。
まず、1章で紹介したMNISTデータセットからマクロ(VBA)を使って抽出します。
lngMaxNum = 10000
とし、59行目のCase文は先ほどと同じように以下のようにします。
Case 2, 5
そして、マクロを実行すると、2と5だけのデータが1854個抽出できました。
2章では191個ですから、ほぼ10倍のデータ数です。
これを「学習データ」シートにコピー&ペーストして、その増えた分に相当する「学習計算」シートの枠も増やしました。
Qtの計算式もそれに合わせて変更することを忘れずに。
私が作ったファイルは最初に紹介したGitHubに以下のファイルを置いておきます。
(※ファイルサイズが61MBあり、ダウンロードに時間がかかります)
cnn(2,5)_p_10000.xlsx
では、ソルバー計算で、「制約のない変数を非負数にする」にチェックを入れて計算してみます。要するに重みとバイアスを正の値にします。
これは、2章で成績が良かったのでそうしました。
結果、下図のようになりました。
この計算時間は何と12時間もかかってしまいました。
(図04-01)
データ総数1854個で、正解率は92.7% でした。
この図だけ見ると、ズラッと正解が並んでいるように見えますが、下の方にスクロールすると結構NGが目立ちます。
残念ながらイマイチの結果でしたね。
今までのセオリー通りならば、正解率はもっと上がっても良いはずですが、逆に下がってしまいました。
もしかしたら、前回記事で説明したように最小解ではなく、極小解だったのかも知れません。
でも、明らかに何かがおかしいぞ?!
根本的に何か間違えているかもしれないと思い始めたので、別の方法を探ってみることにしました。
5.画像を前処理で圧縮して出力層を増やしてみる
2章の畳み込みニューラルネットワーク(CNN)では、出力層のニューロン(ノード)は2つでした。
つまり0~9の数値のうち、2文字までしか判定できませんでした。
それではディープラーニングを実験するには少なすぎる気がしました。
これは、既に述べたように、Excelのソルバーが200個までのパラメータしか対応できないためにそうなってしまうのです。
その制約の中で出力層のニューロン(ノード)を増やすためには、重みパラメータの数を減らさねばなりません。
ならば、28×28 pixel の画像を前処理して、14×14 pixel にする実験をしてみます。
5-1. Maxプーリングで画像圧縮してみる
では、1章で作ったMNISTデータをコピーした新たなファイルを作り、それを作り変えて視覚化してみます。
このExcelデータは、最初に述べたGitHubに以下のファイルで置いておきます。
マクロ無しブックですので、マクロが必要ならば個人で入れてください。
pixel_image(MaxPool)(all)1000.xlsx
まず、下図の様に、28×28 pixel のMNIST元データをいきなり2×2マスのMaxプーリング処理します。
下図の4行目では、後でマクロを組み易くするためにセル列の数を把握するための数列を表示していますが無視してよいです。
(図05-01)
このように、14×14 pixel まで凝縮できました。
ただ、このままだと文字の線が太すぎたり、薄い色の部分が残っていたりして無駄が多いので、そぎ落としてスリム化したいと思います。
そこで、ディープラーニング用語でよく出てくる ReLuという方式を使ってスリム化してみます。
ReLuとは、Rectified Linear Unit の略で、ランプ関数というらしいです。
詳しくは先に紹介した参考書「Excelでわかるディープラーニング超入門」に分かり易く解説されていますので参照してみてください。
簡単に言うと、閾値以下ではゼロを出力し、閾値以上になったらその数値をそのまま出力するというだけの関数です。
シグモイド関数より単純で計算が速いです。
ReLuを使えば、小さい数値を無視してカットすることができます。
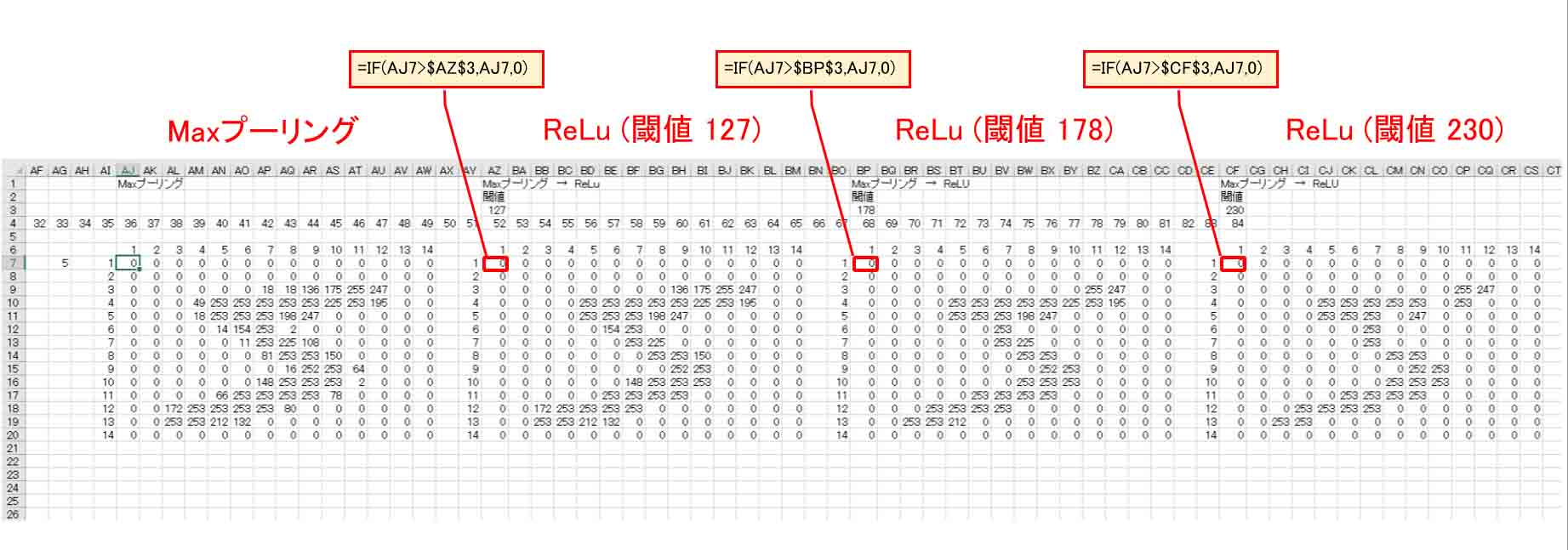
Excelで組むと下図のようになります。
(図05-02)
要するに、単なるIF文ですね。
画素は0~255の範囲なので、閾値50%相当の127、70%相当の178、90%相当の230 に分けてみました。
そして、数値だけでは解りにくいので、セルの背景色を使って視覚化します。
1章で紹介したマクロ(VBA)を更に改変して、以下のようにプログラミングしてみました。
Sub DisplayPixelImage()
Dim bytTmpData As Byte
Dim i, j, k As Long
Dim kk As Byte
Dim lngXcel As Long
Dim lngYcel As Long
Dim lngXStartCelAry() As Long
Dim lngPixSize As Long
Dim lngMax As Long
lngPixSize = 14
lngMax = 1000
ReDim lngXStartCelAry(0 To 3)
For kk = 0 To 3
lngXStartCelAry(kk) = 16 * kk + 36
lngXcel = lngXStartCelAry(kk)
lngYcel = 7
bytTmpData = 0
For k = 1 To lngMax
For j = 1 To lngPixSize
For i = 1 To lngPixSize
bytTmpData = Worksheets("Sheet1").Cells(lngYcel, lngXcel).Value
Worksheets("Sheet2").Cells(lngYcel, lngXcel).Interior.Color = RGB(bytTmpData, bytTmpData, bytTmpData)
lngXcel = lngXcel + 1
Next i
lngXcel = lngXStartCelAry(kk)
lngYcel = lngYcel + 1
Next j
lngYcel = lngYcel + lngPixSize + 2
Next k
Next kk
End Sub
このVBAプログラムでは、Sheet1にMNISTの元データがあり、Sheet2に視覚化画像を出力するように作りました。
よって、新たにSheet2を作成して、このマクロ(VBA)を実行すると、下図の様に表示されます。
(図05-03)
我ながらなかなか良い出来で出力できました。
これを見ると、Maxプーリングというものは、画像を簡単な計算で凝縮してくれるので便利ですね。
ただ、そのままだと線が少し太すぎるので、ReLUを使って閾値を上げてやると、見事に線が細くなってそぎ落とされていますね。
特に4の数字を見ると良くわかります。
閾値178が良さげです。
ただ、MNISTデータ779番目を見てみると、下図の様になります。
(図05-04)
閾値127で人間の目でかろうじて5と判別できるけど、閾値178は3と間違えるかもしれません。
一番右の閾値230では人間が見ても判別不可能ですね。
では今度は、922番目を見てみると、下図のようになります。
(図05-05)
閾値178までは6と判断してしまいそうですが、閾値230までいけば5と判断できそうです。
こうやって見ると、閾値の適正値はなかなか難しいですね。
本来ならば画像を前処理しない方が良いと思いますが、Excelの制約上仕方ありません。
結局、どれが最適かは今の自分には判断できませんが、ここでは閾値をとりあえず230、つまり90%で実験していきます。
ところで、この実験最中にTwitterで話題になっていた情報誌、CQ出版の「インターフェース2020年11月号」を買ってしまいました。
ESP32を使った画像処理や、Maxプーリングによる画像圧縮なども掲載されていて、即買いしてしまいました。
Twitterでいろいろと大変お世話になっている方々も執筆されているのでお勧めです。
ただ、今の私にはまだ難解すぎて、Maxプーリングで画像処理するだけで精一杯でした。
5-2. ニューロン(ノード)数および重みとバイアスの個数を決定する
では、MNIST画像が圧縮できたので、ソルバーのパラメータ200以内という制約で、重みやバイアスをいくつ作れば良いかを計算します。
まず、畳み込み層①は最低3ニューロン必要です。
その重みフィルターは、前処理で画像を圧縮しているので、4×4 マスにします。
3章で重み(W)の性質が分かったので、14×14画像には4×4マスの重みでも大丈夫だろうという判断です。
逆にそれ以下では正常な学習ができないだろうと思ったので、必要最低限というところですね。
すると、畳み込み層①のパラメータ数は、
重み(W): 4×4×3 = 48
バイアス(b): 3
合計: 48 + 3 = 51
となります。
次に、畳み込み層①だけでは凝縮が足りないので、畳み込み層②を作ります。
重みは3×3マスで充分で、ニューロン(ノード)は3つなので、畳み込み層②のパラメータ数は、
重み(W): 3×3×3 = 27
バイアス(b): 3
合計: 27 + 3 = 30
となります。
こうすると、後で紹介しているものを見れば分かるのですが、最終的に1ニューロン(ノード)あたり、2×2マスまで凝縮されます。
出力層については、全てのニューロン(ノード)に対して重みを付けます。
すると、0~9 の10種類、つまり、出力層10ニューロンを作るとすると、出力層のパラメータ数は、
重み(W): 2×2×3×10 = 120
バイアス(b): 10
合計: 120 + 10 = 130
となります。
affine(全結合)するので膨大な数になりますね。
結果、全パラメータ合計は、
51 + 30 + 130 = 211
となってしまい、Excelのソルバー制約を超えてしまいました。
ならば、削ることできるところと言えば、出力層しかありません。
そこで、出力層のニューロンを10個から9個に変更します。
つまり、0という数字の判定をカットし、1~9 までの9種の判定にします。
すると、パラメータ総数は 198個となり、ギリギリ制約を満たせました。
これで、各パラメータの数が決まりました。
5-3. 圧縮した画像から畳み込みニューラルネットワークを作る
では、ニューロンや重み、バイアスの数が決まったところで、畳み込みニューラルネットワークを組んでみます。
まずは、新たなExcelファイルを作り、1章と同じように「学習データ」というシートを作って置きます。
そして、1章で使ったマクロ(VBA)を使って、MNISTデータセットの1000個の中から1~9の数値だけを抽出します。
lngMaxNum = 1000
とし、59行目のCase文は、
Case 1, 2, 3, 4, 5, 6, 7, 8, 9
として、マクロを実行すると抽出できます。
この抽出完了したファイルは、先に紹介したGitHubに以下のファイルを置いておきます。
(※ファイルサイズが36MBあり、ダウンロードに時間がかかります)
cnn(1-9)_n_1000.xlsx
次に「学習計算」というシートを作成し、下図の様にリンクさせて、28×28 pixel の画像を前処理で2×2のMaxプーリング処理します。
Maxプーリングしても、0~255という値なので、2章で紹介したことと同様に割値のこころで 1/255 = 0.00392 という数値を作って置き、全てのセルに掛け合わせておきます。
(図05-10)
次に、先ほど述べたようにReLu関数を使って、小さい数値を無視してそぎ落とします。
下図の様に閾値は0.9とします。
(図05-11)
これで画像の前処理の圧縮が済んだので、ここから一つ目の畳み込み層①を作ります。
先ほど決めた重み(W)の数に従って、4×4マスでニューロン(ノード)を3つの重み(W)と閾値(バイアス)を乱数で作ります。
この乱数は2章と同じように割値の0.2を掛けて置きます。
そして、下図の様に畳み込み層をストライド1でシグモイド関数出力させます。
ストライド1にするとOFFSET関数不要なので簡単ですね。
(図05-12)
次に、一つ目のMaxプーリング層①を作ります。
畳み込み層①は11×11マスなので、2×2マスのMaxプーリングすると、11行や11列が問題になって来ます。
ですが、仮想の12列は空白のゼロ値なので、そのままOFFSET関数でMaxプーリングして良いと思います。(あくまで個人的想像です。間違えていたらゴメンナサイ)
(図05-13)
これで、6×6マスまで縮小できましたが、まだ多すぎるので、2つ目の畳み込み層②とMaxプーリング層②を作ります。
先ほど計算したように、畳み込み層②の重み(W)は3×3マスにします。
そして、下図の様にストライド1でシグモイド関数出力させると、4×4マスになります。
そして、そこから下図の様に2×2でMaxプーリングさせると、最終的に2×2マスまで縮小できました。
(図05-14)
ここまで縮小できれば十分なので、これから全結合(affine)して出力層を作ります。
出力層はニューロン(ノード)が多いと厄介です。
1~9の数字、計9個のニューロンを全結合(affine)させるため、下図の様に重み(W)とバイアスを作ります。
画像に収まらないのでハミ出ています。
(図05-15)
そして、出力では0を無視して空白にして、1~9までシグモイド関数出力します。
誤差やQtは2章と同じです。
これで画像を前処理した畳み込みニューラルネットワーク(CNN)が完成しました。
重みやバイアスを乱数にしているとはいえ、Qt値が3000を超えてしまいました。
ここまで大きい数値になると、ソルバー計算に膨大な時間が取られてしまいます。
(※実は後で気付いたのですが、出力層がシグモイド出力だったことが問題でした。
ここは本来、ソフトマックス関数でないとダメなんです。それについては後で述べます。)
5-4. ソルバー計算で学習させた結果
では、ソルバーで計算させてみます。
Qt値を選択した状態でExcelのソルバーを起動し、下図の様にします。
今後の実験の都合上、ここでは「制約のない変数を非負数にする」のチェックを外して、負の値を許容します。
(図05-16)
変数セルの変更欄は以下です。
$BS$54:$BV$65,$BW$54,$BW$58,$BW$62,$EI$57:$EK$65,$EL$57,$EL$60,$EL$63,$EV$12:$EW$65,$EX$12,$EX$18,$EX$24,$EX$30,$EX$36,$EX$42,$EX$48,$EX$54,$EX$60
学習結果は下図のようになりました。
(図05-17)
正解率が57.3%という悪い結果になってしまいました。
これでは正常な判定はできませんね。
全く使えないデータです。
学習時間は約6時間でした。
Qt値は519という値までしか収束しませんでした。
これは何かを間違えていそうですね。
実は後々分かったことですが、出力層がソフトマックスでないことが原因です。
その原因が分かる前にまず疑問に思ったのは、畳み込み層のニューロン(ノード)が少なすぎるからだと思ったので、次では畳み込み層のニューロン(ノード)を増やしてみます。
6.畳み込み層のニューロン(ノード)を増やす
5章では、出力層のニューロン(ノード)を9個まで増やしてみましたが、判定結果が良くありませんでした。
その原因は8章で述べているようにソフトマックス関数を使っていなかったことなのですが、その原因をつかむ前に疑問に思ったことは、畳み込み層①の段階で、ニューロン(ノード)数が3個では少ないからだと想像しました。
では、今度は畳み込み層①のニューロン(ノード)数を増やしてみます。
そうすると、当然、ソルバー計算の制限により出力層のニューロン(ノード)数が減るので、5章の結果との比較検証はできませんが、何はともあれとりあえず片っ端からやってみます。
このファイルは、GitHubの中に置いておきます。
(※ファイルサイズが13MBあり、ダウンロードに時間がかかります)
cnn(2,3,5)(5node)_n_1000.xlsx
予め枠を増やして置き、下図の様にニューロン(ノード)を5つに増やします。
すると、出力層のニューロンは3つが限界なので、2と3と5を判定することにします。
先ほどと同じように、MNISTデータセット1000個の中から2,3,5の数字を抽出します。
1章のマクロ(VBA)で
lngMaxNum = 1000
とし、59行目のCase文は、
Case 2, 3, 5
として実行させて、学習データを作ります。
そして、重みと畳み込み層①、Maxプーリング層①は下図の感じです。
重みとバイアスには乱数を入力しておきます。
計算式は今までと同様なので割愛します。
(図06-01)
二つ目の畳み込み層②とMaxプーリング層②は以下のようになります。
そして、出力層も以下のようになります。
(図06-02)
6-1. ソルバー計算で学習させた結果
では、ソルバー計算させてみます。
例のごとく、「制約のない変数を非負数にする」のチェックを外して、負の値を許容します。
すると、結果はこうなりました。
(図06-03)
凄いですね。
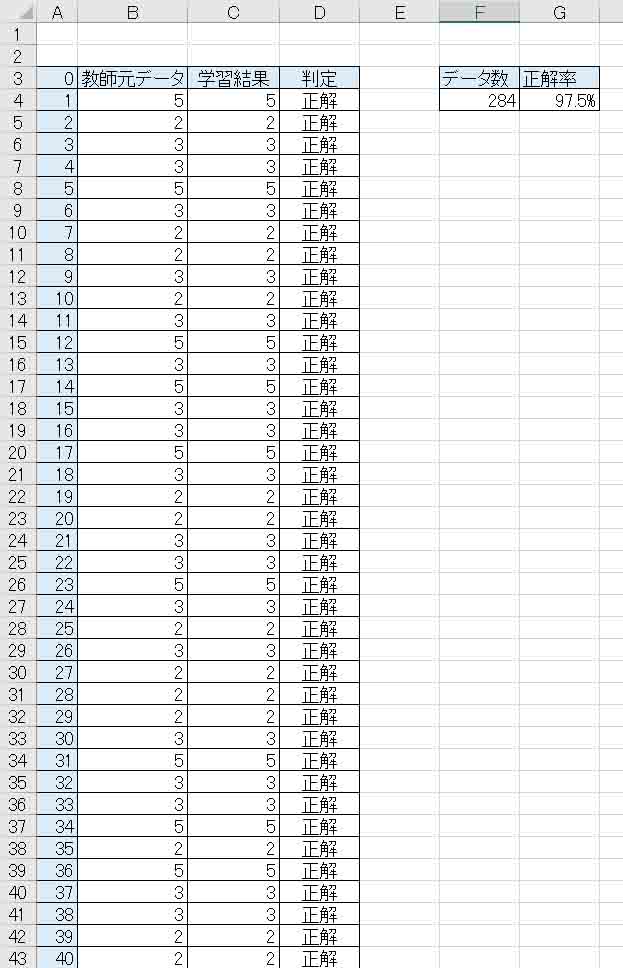
ズラーッと正解が並んでいます。
学習データは284中、正解率は97.5%まで上がりました。
計算時間は私のパソコン環境で4時間50分くらいかかりました。
Qt値も11にまで収束しました。11っていうのは学習がかなりうまく行った証拠です。
素晴らしい!!!
ここまで正解率が上がると、使えるデータとなりそうです。
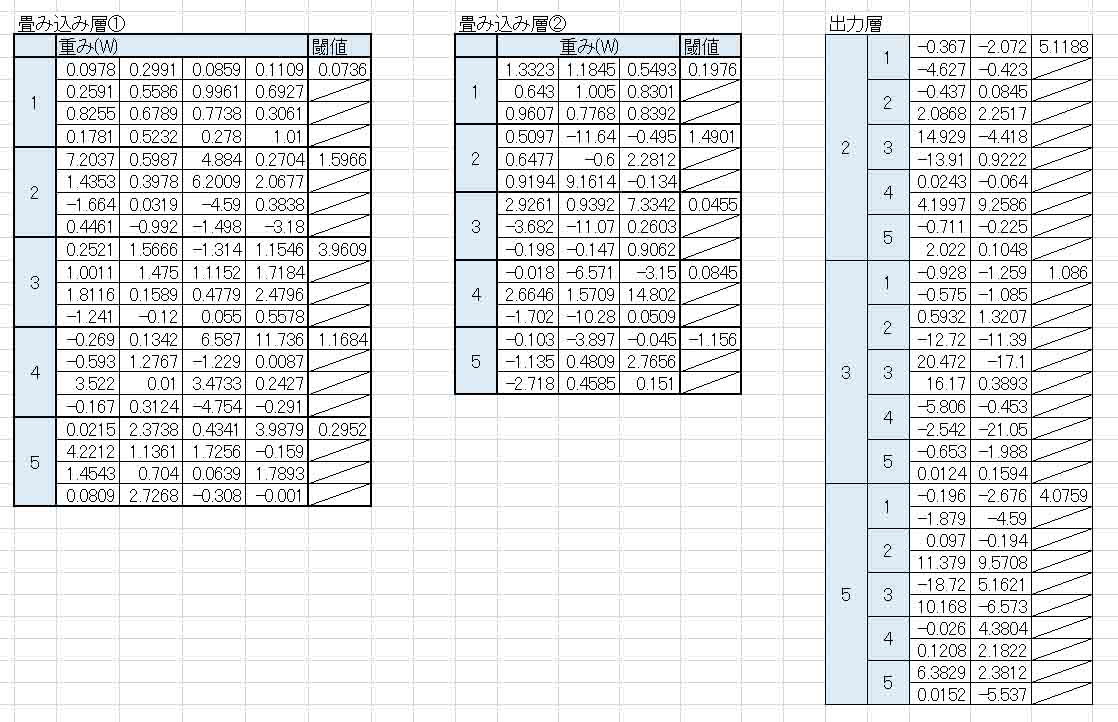
さて、この学習で得られた重みとバイアスの値を見てみると、以下のようになりました。
(図06-04)
負の値を許容すると、重みの意味がさっぱり分からなくなりますね。
ところで、これをずっと眺めていて、ふと気付いたことがありました。
重みとバイアスに負の値を許容するなら、他のパラメータも負の値を許容しないと正常な判定ができないのではないかと思ったんです。
そこで、次の方法を試してみます。
7.活性化関数にtanhを使ってみる
前章で述べたように、一つの疑問が出てきました。
Excelのソルバー計算で、目的値に負の値を許容しているのに、これまでは畳み込み演算でシグモイド関数を使って正の値にしているというのは、学習の精度が劣るのではないかと思い至りました。
そこで、いろいろ調べると、負の値も出力できる活性化関数に tanh というものがあることを知りました。
tanhとは、Hyperbolic Tangent(双曲線正接)というものです。
これは高校数学でも習わないらしいので、正直言ってどういう理屈なのか私にはサッパリ分かりません。
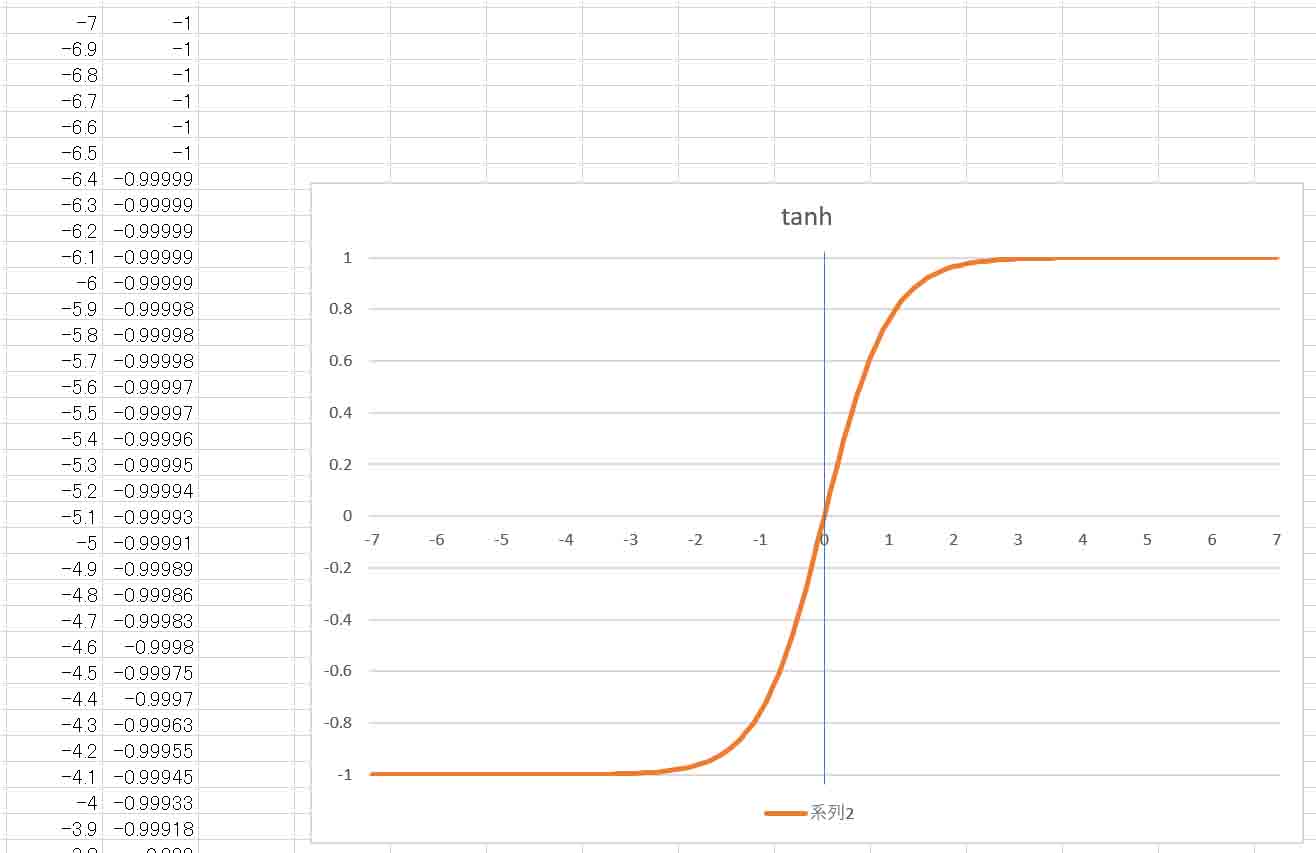
ただ、y = tanh(x) とした場合、xがどんな値でも -1 ~ +1 の範囲内で収まるのです。
Excelでグラフを作ってみると、こんな感じです。
(図07-01)
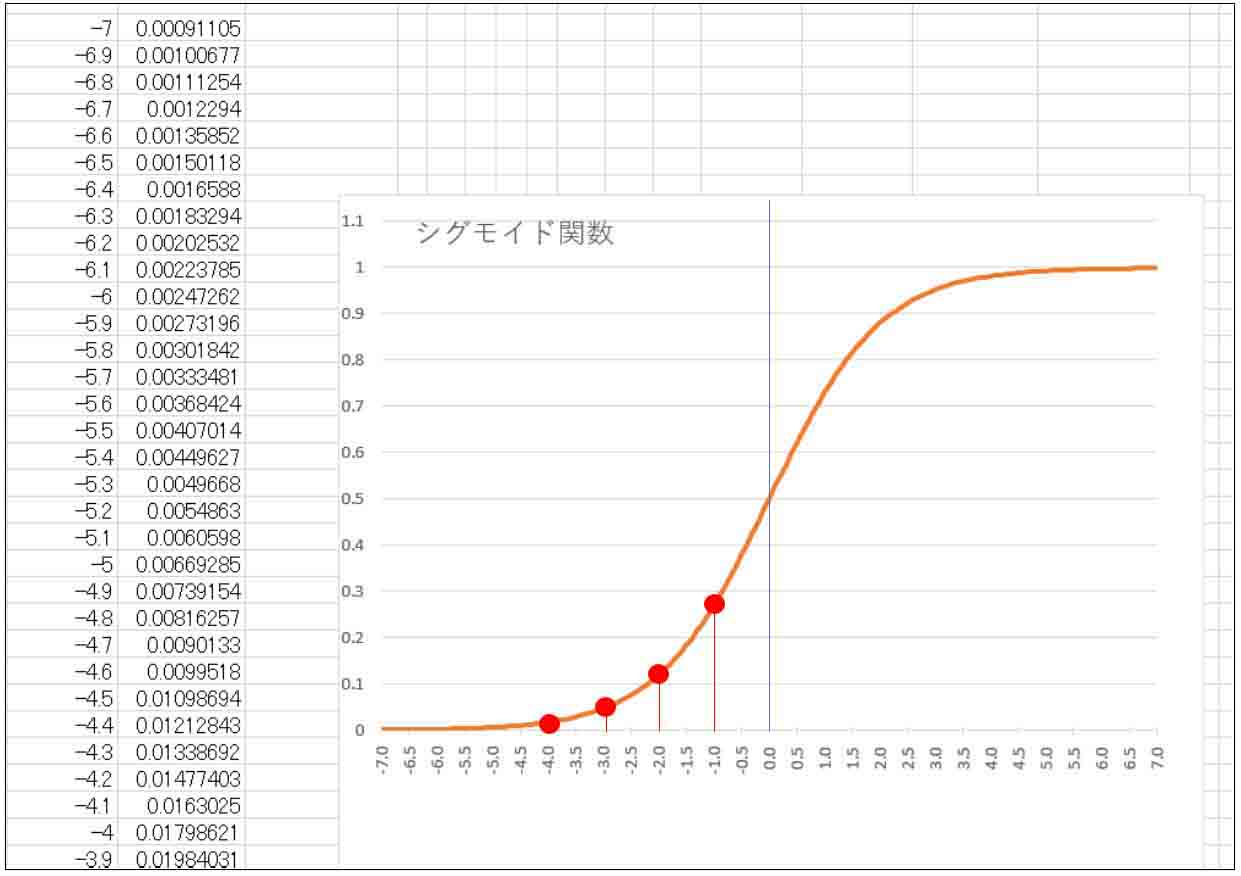
因みに、比較のために以前の記事で紹介したシグモイド関数のグラフは以下の感じです。
(図07-02)
tanh関数とシグモイド関数は形が似ていますが、tanhの方が傾きが急で、負の値を出力するという所が特徴です。
これは、ソルバー計算の負の値許容とうまくマッチしそうだと考えました。
そこで、成績が悪かった5章の1~9の数字判定の畳み込みニューラルネットワークにtanhを使って改善するか実験してみたいと思います。
このファイルは、GitHubの中に置いておきます。
(※ファイルサイズが36MBあり、ダウンロードに時間がかかります)
cnn(1-9)(tanh)_n_1000.xlsx
まず、下図の様に、畳み込み層①のシグモイド出力関数を外して、SUMPRODUCT関数からバイアスを引いただけの値とします。つまり全結合(affine)と同じです。
バイアス(閾値)以下の場合は負の値になり、それ以上になると正の値になります。
そして、Maxプーリング層①を作り、そこにtanh関数を適用します。
(図07-03)
畳み込み層でtanhを適用しても良いのですが、そうするとtanh計算の量が多すぎるので、Maxプーリング層でtanhを適用した方が計算が速いと思います。
同じく、畳み込み層②とMaxプーリング層②を作り、tanhを適用します。
(図07-04)
出力層は確率計算の為に必ず正の値にしなければならないので、シグモイド関数出力のままにします。
では、ソルバーを起動し、「制約のない変数を非負数にする」のチェックを外し、負の値を許容して計算させます。
結果、以下のようになりました。
(図07-05)
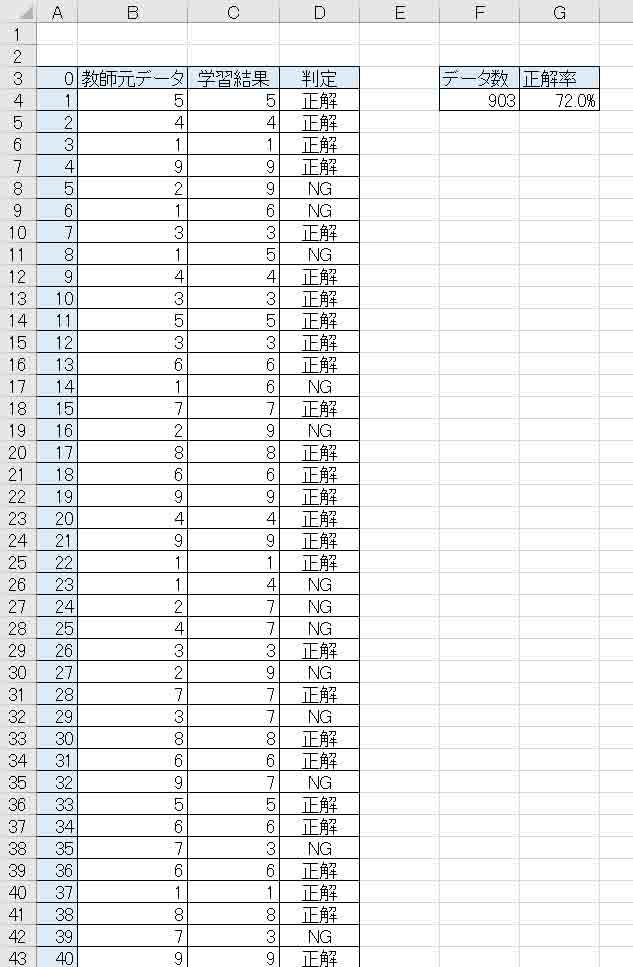
5章では正解率が約57%ほどでしたが、今回は72%となり、明らかに正解率が上がりました。
計算時間は私のパソコン環境で約11時間かかりました。
Qt値は352に収束しました。
このことから、畳み込み層やMaxプーリング層の段階では負の値を許容して、tanhを適用した方が明らかに良いですね。
ただ、正解率が上がったとはいえ、72%では実用できません。
パッと見て分かる通り、NGの数が多すぎます。
でも、ちょっと希望が見えてきました。
さて、ここでいろいろ調べていると、またふと気付いたことがありました。
それはソフトマックス(softmax)関数です。
次ではそれを紹介します。
8.出力層のシグモイド関数をソフトマックス関数に変更してみる
さて、いろいろ実験していると、ふと気が付きました。
今まで、畳み込みニューラルネットワーク(CNN)の出力層はシグモイド関数を使っていましたが、ネットの情報を見てみると、ほとんどが出力層はソフトマックス(softmax)関数で出力すると書かれていました。
最初に紹介した書籍「Excelでわかるディープラーニング超入門」を題材にしてディープラーニングを実験していて、そこにはソフトマックス関数については書かれていなかったので、私はソフトマックス関数についてはシグモイド関数のことと勝手に思い込んでいたので、スルーしていました。
でも、ちゃんと調べてみると、ソフトマックス関数は複数ニューロン(ノード)出力の場合に用いるという情報でした。
ということは、今まで自分は大きな間違えていたのかも知れません。
ならば、ソフトマックス関数で計算してみて、シグモイド関数とどれだけ違いがあるのかを探ってみたいと思います。
8-1. ソフトマックス(softmax)関数とは
ソフトマックス(softmax)関数とは、すべての出力の数値を合計すると1になるような関数です。
そうすれば、それぞれ出力された結果を確率として処理できるということだそうです。
n個の入力をそれぞれ、X1, X2, X3,……., Xn とすれると、X2 のソフトマックス出力は、
(X2のsoftmax出力) = EXP(X2) / (EXP(X1) + EXP(X2) + EXP(X3) +……+EXP(Xn))
となります。
いろいろ調べると、入力が2値(例えばX0とX1のみ)の場合、ソフトマックス関数はシグモイド関数と同じ値になるとのことです。
確かに約分すればそうなりますね。
3値以上の場合はシグモイド関数にはなりません。
ならば、これが原因で今まで学習の正解率を上げることができなかったわけですね。
ところで、ソフトマックス関数はなぜネイピア数(自然対数の底)EXPを使うのでしょうか?
これはネット上にいろいろ情報があるのですが、まず1つにネイピア数を使った以下の式
y = EXP(x)
では、xが負の値でもyは正の値を取るという所が、確率を求める場合には好都合だからです。
そして、もう一つ重要な特徴として、微分しても積分しても同じ式 y = EXP(x) になるそうです。
Excelでは、ソルバーを使って最小値(実際は極小値)になるように計算させていますが、微分して関数の接線の傾きの最小値を求めていることと同等らしいので、値が変化しない方が無難ですよね。
以上からネイピア数を使うと好都合なのだと個人的に理解しておくことにします。
(参考サイト)
8-2. ソフトマックス関数で出力層を構成してみる
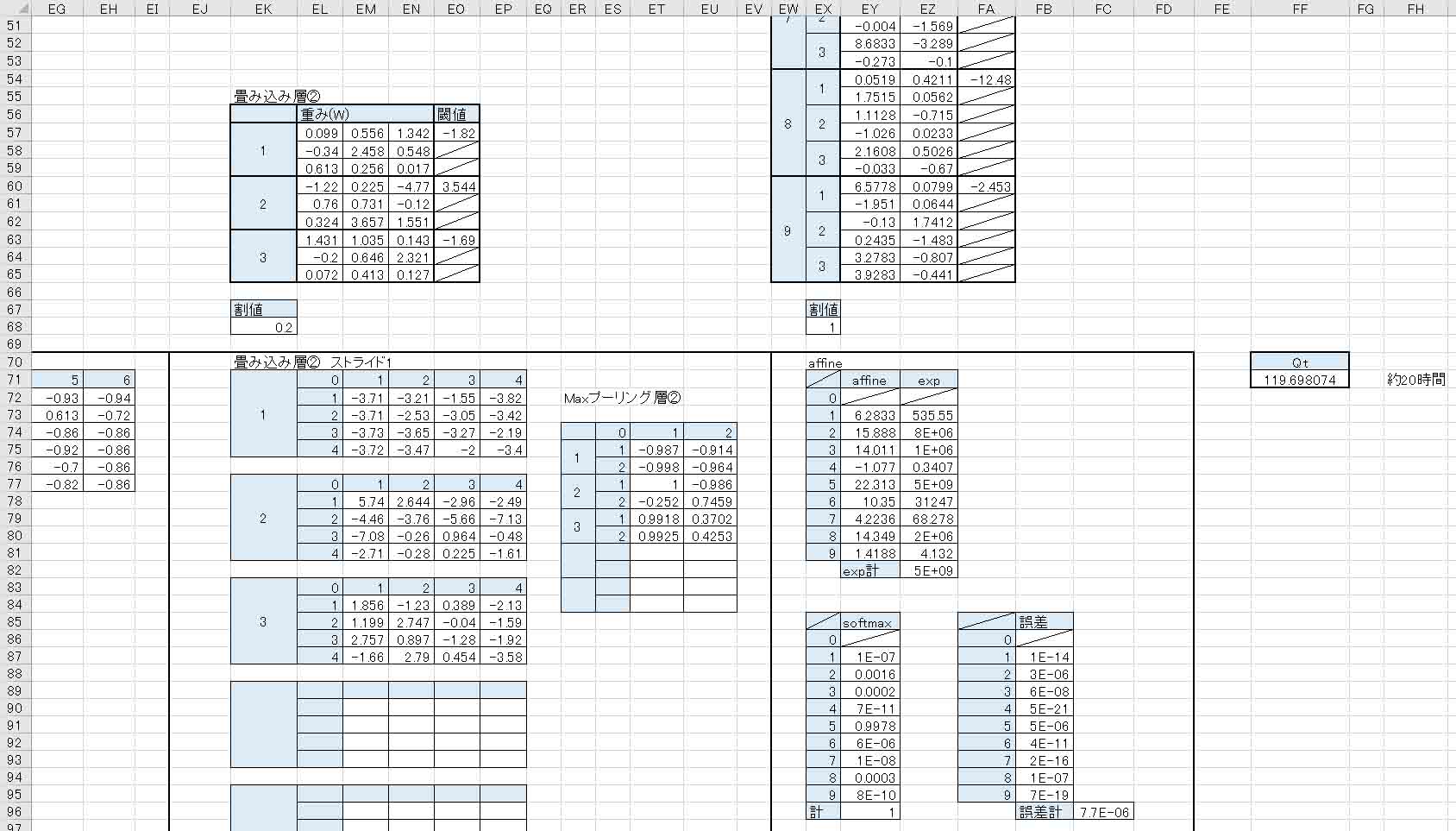
では、ソフトマックス関数の概要が分かったところで、今までやってきたシグモイド関数の出力層をソフトマックス関数に組み直してみます。
このファイルは、GitHubの中に置いておきます。
(※ファイルサイズが38MBあり、ダウンロードに時間がかかります)
cnn(1-9)(softmax)_n_1000.xlsx
下図の様な感じで、表を追加しました。
(図08-01)
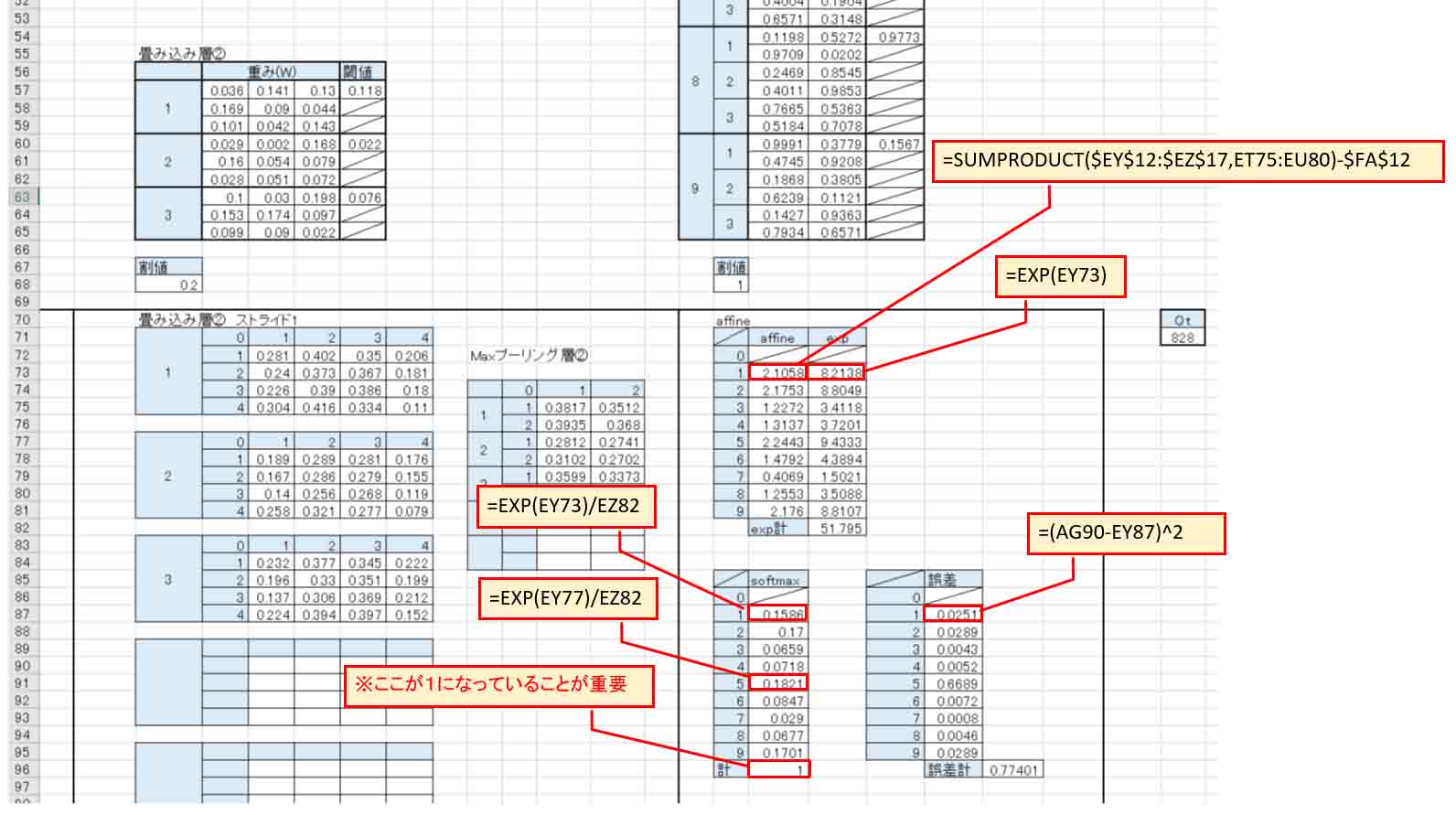
まず、Maxプーリング層と出力層の重み(W)とバイアス(閾値)をaffine(全結合)します。
その後、それをネイピア数(EXP)関数に置き換えて、その合計(exp計)も計算しておきます。
そして、文字1の出力層は
=EXP(EY73)/EZ82
文字2のところは
=EXP(EY74)/EZ82
という風に分母が出力の合計値になります。
ここは絶対参照にしない様にします。
そうしないと、表全体をコピーする時にうまく参照できません。
Twitterでもつぶやいていましたが、私が失敗したのは、まさに分母を絶対参照にしてしまって、他の全データもその値を参照してしまって、分母が1になっていませんでした。
それを気付かずに30時間も学習させてしまった事でした。
貴重な時間をドブに捨ててしまいました。
ソフトマックス関数の出力合計が1になることのもう一つ重要な利点として、重みとバイアスの初期値に乱数を適用しても、平方誤差の総合計であるQt値の初期値が低く抑えられるという点にあります。
今回のこの場合のQtのスタート値は830程度ですから、5章の3000越えと比べると学習時間は大幅に短縮できますね。
8-3. ソルバー計算で学習させた結果
では、ソルバーで「制約のない変数を非負数にする」のチェックを外して負の値を許容して計算させてみます。
結果、以下のようになりました。
(図08-02)
計算時間は私のパソコン環境で20時間かかりました。
Qt値は830から約119に収束しました。
正直、もっと収束して欲しいところですね。
今回は単なる極小解かも知れません。
重みやバイアス、Maxプーリング層出力、出力層のaffineでは、いい具合に負の値が出ています。
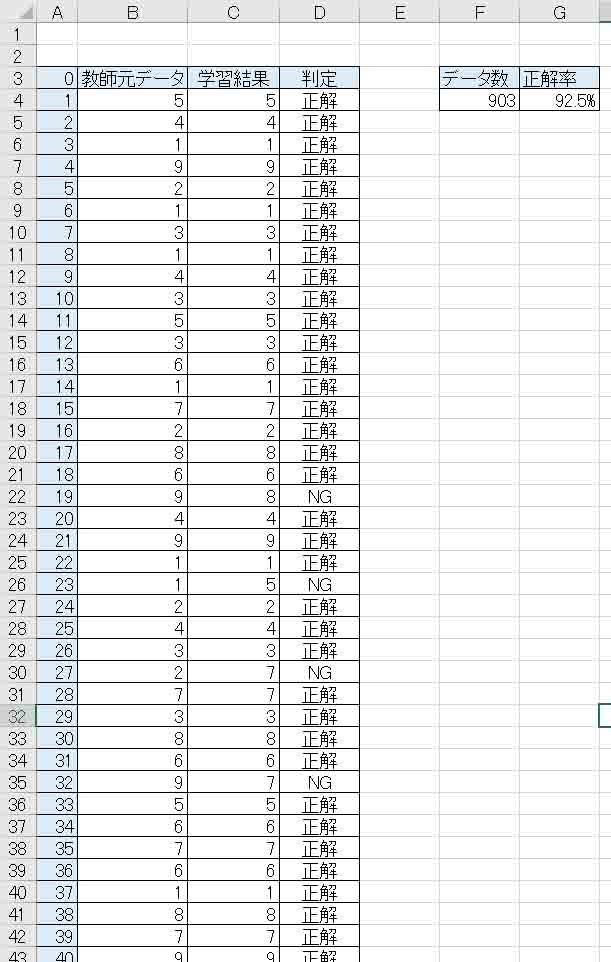
集計結果は以下のようになりました。
(図08-03)
やった!
畳み込み層のニューロン(ノード)数が3つでも92.5%という正解率を叩き出しました!
予想ではもうちょっと低いかと思ったのですが、なかなか良い感じです。
でも、92.5%ではやはりNGのところが目立ちますね。
97%を超えると使えるデータになるのですが、これでも上出来です。
もっとパラメータのスタート値をいろいろ変えて、何度もソルバー計算をやり直せば良い値が出るかもしれませんね。
いずれにしても、7章の72%よりもグーンと正解率が上がったので、今までうまく行かなかった全ての原因はこの出力層のソフトマックス関数だったことが分かりました。
これで解決です!
本当は、今までの計算を全てソフトマックスに変えてやり直したいのですが、Excelのソルバー計算があまりにも時間がかかって、他の作業ができないので、今回はこれくらいで留めておきます。
9.Excelで計算するディープラーニングの限界
以上から分かるように、さすがに28×28 pixel の畳み込みニューラルネットワーク(CNN)の計算はExcelでは無理がありますね。
たかだか200程度の学習データだけで、ソルバー解決が30時間くらいかかることもあり、データが最適でないと再度ソルバー計算させることを繰り返すと、その間、Excelで他の作業が一切できなくなってしまいます。
せめてソルバー計算はExcel作業と切り離してできるようになるといいなと思います。
そこはMicrosoftさんにお願いするしか無いですね。
それに、たまに30時間以上経っても計算完了しない時がありますが、その時は大抵Windowsアップデートが裏で動いていて、再起動を待つ状態になっている時です。
これにはいつも腹が立ちますね。
とにかく、Excelの動作がいつもと違うなと思った時にはWindowsアップデートがかかっていて、素直に再起動か電源を落とした方が良いということは覚えておいた方が良いと思います。
いずれにせよ、Excelでディープラーニングをやるのは、初期の導入段階のお勉強くらいですね。
本格的にガツガツやるなら、専用のツールを使った方が断然良いです。
ディープラーニングの勉強を始めた頃は、Excelのソルバー計算に相当するアルゴリズムを自分で作って、マイコンで計算させてみようと思ったのですが、マイコンより遙かに高性能なノートパソコンのExcel計算でも30時間を超えたりするのを何回も繰り返していると、こんな計算はAIクラウドツールを使ってサクッとやった方が遙かに賢いなと思うに至りました。
ただ、全く無知な状態からディープラーニングを勉強するにはExcelはとっても良いツールだと思います。
一目瞭然で視覚化できて、仕組みも良くわかり、改めて優れたソフトだと思いました。
書籍だけ読んだだけでは直ぐに投げ出していたでしょうね。
結局はなんだかんだ言っても、Excelスゴイ! っていうことです。
そもそも、Excelでディープラーニングなんて出来るのかいな? と最初は思っていたのですが、最初に紹介した書籍「Excelでわかるディープラーニング超入門」を呼んで、とても分かり易かったので、これは出来る! と思って取り掛かったわけです。
Excelも凄いのですが、この本が無かったらExcelでディープラーニングやろうとは思わなかったです。
こういう優れた書籍には感謝したいですね。
まとめ
以上より、画素数の多い画像の場合は、畳み込みニューラルネットワーク(CNN)を使うということが分かりました。
ただ、手書き数字データセットのMNISTを学習させるには、Excelではさすがに無理がありました。
でも、MNIST画像を前処理で圧縮させてやれば、9文字まで出力させることができましたし、Excelの方が視覚的に理解し易かったです。
重みと畳み込み演算の特徴や、ニューロンの数の決め方、Maxプーリングによる画像圧縮、活性化関数の特徴などをExcelだからこそ肌で感じることができました。
今回の勉強で学んだことは、
●多量の画素のデータを学習させるには畳み込みニューラルネットワークを組む。
●入力層のデータが多くても、前処理でMaxプーリングを使って画像を圧縮すると良い。
●活性化関数ReLuを使うと、無駄な部分のデータをカットできる。
●重みやバイアスは負の値を許容する時、活性化関数はシグモイド関数よりもtanhを使った方が良い。
●出力層のニューロンが3つ以上の場合はソフトマックス関数にすべし。
●最初の畳み込み層のニューロンは多いほど良い。
●ExcelでCNNは厳しいが、仕組みを視覚的に肌で感じるには最適。
●ExcelでMNISTデータセットを学習させるなら、1回の学習で24時間越えを覚悟しておく。
というところでしょうか。
ド初心者から勉強し始めて、今までの記事3回シリーズでだいぶ畳み込みニューラルネットワークおよびディープラーニングが理解できるようになりました。
関数やデータの決め方にも迷いが無くなったと思います。
もうExcelでは限界なので、次回はもっと計算が速く、多くのパラメータを扱うことができるツールを使ってみたいと思います。
ということで、今回はここまでです。
ではまた・・・。
Amazon.co.jp 当ブログのおすすめ











コメント