こんばんは。
今回は今までとは趣向を変えて、ついにディープラーニングとニューラルネットワークに挑戦してみることにしました。
その分野は超ド初心者なので、細かいことはサッパリ分かりませんし、何の知識もありませんが、書籍やネットの情報に頼りながらゼロからプログラミングしていくことにチャレンジしてみます。
プログラミングと言っても、ニューラルネットワークが何なのかも分かっていないので、まずはMicrosoft Excelでシミュレーションしてみました。
ここでは自分流の視点で記事を書いていきます。
間違えや勘違いしていることも多々あると思いますので、そのつもりで読んでいただければと思います。
今まで長い間イメージセンサをWiFiマイコンで駆動して、動画ストリーミング実験をしてきましたが、前回記事で高速カメラストリーミングが実現できて一区切りしたので、いよいよイメージセンサの画像でディープラーニングを使ってみようと思ったわけです。
実は、2年位前から今年こそはディープラーニングを始めるぞと言い続けてきたのですが、ようやく重い腰を上げて取り組み始めたのです。
以前、書籍を斜め読みしたのですが、細かい専門用語にウンザリして、すぐに勉強を止めました。
でも何となくザッと大まかに分かった気でいました。
しかし、今回、いざプログラミングしてみようとすると、どうやって良いかサッパリ分からなかったんです。
それに、自己流で数式や条件式を組んで判定したものと、ニューラルネットワークおよびディープラーニングの判定との根本的な違いが解らなくなってきたのです。
ということで、今回、まずはニューラルネットワークやディープラーニングというものの動作を肌で感じるために、MicrosoftのExcelで体感してみることにしました。
今回は 3×3 pixel の9画素で、〇か×かを判断する超簡単な例を題材にしてみました。
これが驚いたことに、エクセルはなかなかバカにできないですよ!!!
実際に作ってみると、かなり直感的に理解できるようになったんです。
Excelって改めて優れたソフトウェアだなと思いました。
実は既にニューラルネットワークまで実験済みなんです。
ですが、記事にするとメチャメチャ膨大になるので、段階的に分けて記事をアップしていこうと思います。
正直言って、ニューラルネットワークやディープラーニングの勉強ってすごい地味で、ぜんぜん面白くないんですよ。
(あくまで個人的意見です)
書籍を読んでも、直ぐに熟睡できるほど詰まらないので、ディープラーニングの本は不眠症に最適です。
(あくまで個人的意見です)
でも、Excelを使って自分の手で計算式を組んで実験すると、だんだん直感的に理解できるようになってきました。
Excelができる人で、これからディープラーニングを学びたい人にはこの手法はホントおススメですよ。
ということで、まずは勉強の第1弾として、超簡単な 3×3 pixel の画像で、書籍やネットの情報に頼らずに自己流で計算式を作って、○と×の判定をしてみたいと思います。
そして、自己流計算の限界とバイアスやシグモイド関数について気が付いたことをダラダラと述べていきたいと思います。
なお、Excel操作については一切説明していませんのでご了承ください。
- 参考にした書籍
- 自己流サンプルファイル
- 超簡単な3×3 pixel 白黒画像で〇×判定を作る
- まずは自己流計算で〇×を判定してみる
- 自己流計算プログラムにバイアス(閾値)とシグモイド関数を取り入れてみる
- 自己流計算プログラムの限界
- まとめ
【目次】
参考にした書籍
まず、1~2年前に買った超有名なオライリー・ジャパンの以下の書籍です。
【題名】
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
【著者】
斎藤 康毅
正直、これは私には難し過ぎました。
高校数学の微分積分が出てくるし、それにPythonは使ったことないので、余計に難しいです。
ただ、次に紹介する初心者用書籍を参考にExcelで作りながらこの書籍を見返すと、とても良く解るようになってくると思います。
(あくまで個人的意見です)
そこでこれです。
初心者向けで、しかもエクセルで実践してディープラーニング試すことができる以下の書籍を手に入れました。
【題名】
Excelでわかるディープラーニング超入門
【著者】
涌井 良幸、涌井 貞美
●電子書籍Kindle版
●単行本版
これは本当に初心者向けですが、私にはピッタリでした。
もちろん、エクセルがある程度操作できる必要がありますが、先ほどの書籍よりかなり分かり易いです。
ただ、この本は読んだだけではイマイチ分からない部分があるので、実際に自分の手でこの本を参考にExcelで作っていくと、手に取るように理解できるようになりました。
個人的に超おススメです!
この本と共にExcelで作って理解した後、改めて先ほどの本を読み返すとGoodだと思いますよ
自己流サンプルファイル
ここで作った私の自作ExcelファイルはGitHubにアップしておきますので、ダウンロードできます。
あまり期待しないでください。
まだ始めたばかりなので、ニューラルネットワークも組んでないし、ディープラーニングもできない単純な計算式だけです。
今後、勉強が進むにつれて、徐々に新しいファイルアップしていく予定です。
https://github.com/mgo-tec/test_excel_deeplearning
今回は、
my_func01.xlsx
というファイルを使っています。
図の番号とシート名と合わせています。
1.超簡単な3×3 pixel 白黒画像を作る
超簡単な 3×3 pixel (9画素)の白と黒だけの画像を題材とします。
まずは、〇か×のたった2種類の画像判定を考えてみます。
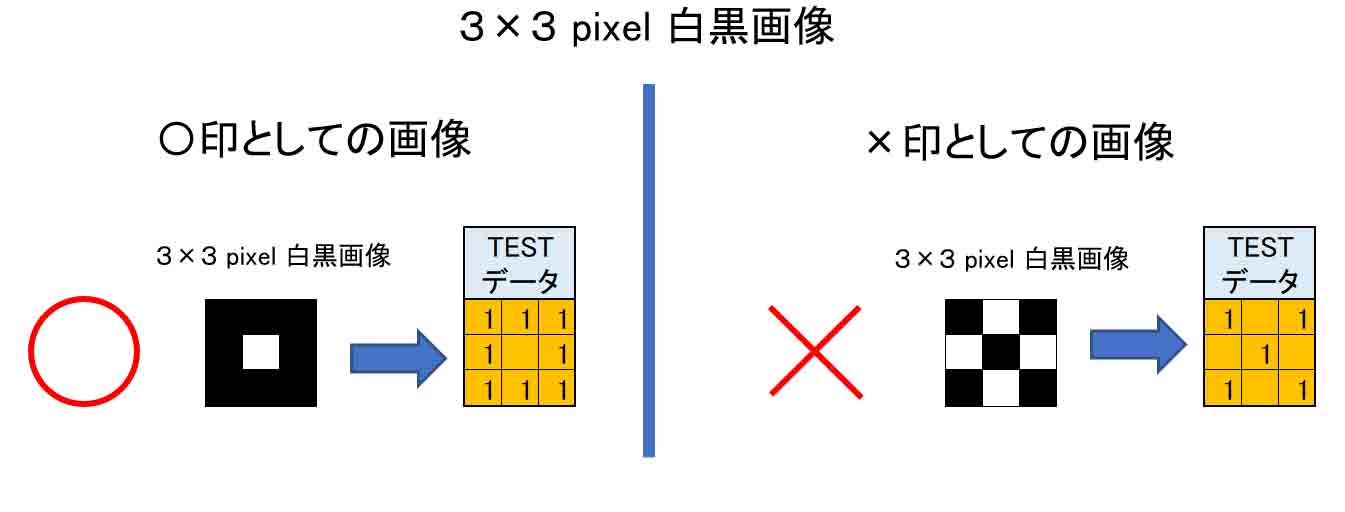
例えば、3×3 pixelのカメラ(イメージセンサ)があったとして、それを画像にすると、単純に考えると以下のように表現できると思います。
(図1_01)
イメージセンサの場合、一般には1画素中に0~255の輝度を表現できますが、ここでは0か1だけで表現します。
エクセルの場合、空白は0と同じなので、ここではあえてゼロと表示しません。
次に、手書き文字の場合、〇や×は以下のようにも表現できると思います。
(図1_02)
特に下の段の場合、○と×の違いは中央の画素が有るか無いかの違いだけです。
こんな感じのデータを題材として、ニューラルネットワークとディープラーニングの勉強を進めていきます。
2.まずは自己流計算で〇×を判定してみる
ニューラルネットワークおよびディープラーニングと普通のプログラムとの違いを明らかにする為、自己流で計算プログラムをエクセルで組んでみて、○×を判定してみました。
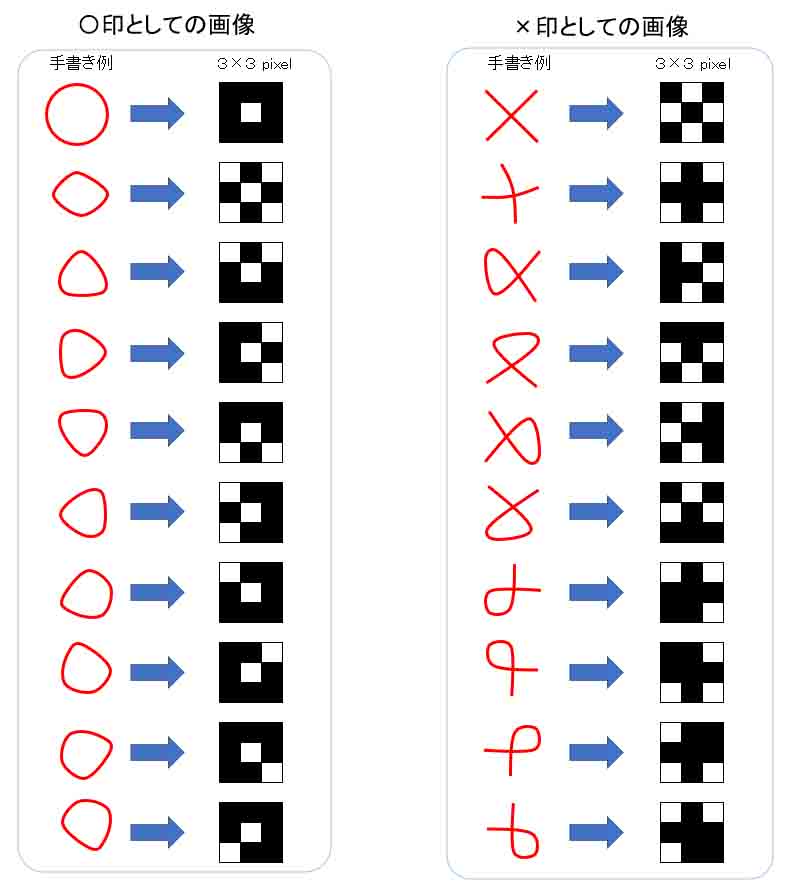
まず、〇として判定する3×3 pixelのサンプル画像を用意します。
これはあくまで、私の独断で決めた画像例です。
(図2_01)
×印は鉛筆で素早く書くときはつながってしまう場合も考えてみました。
場合によってはつながった×印の方が○と捉える人もいると思います。
この10個の例以外にも考えられますが、それについては後で述べます。
とりあえず、この例でエクセルで組んでみます。
このデータをとりあえずここでは「教師データ」としておきます。
そして下図の様に、TESTデータ(X)は入力データとします。
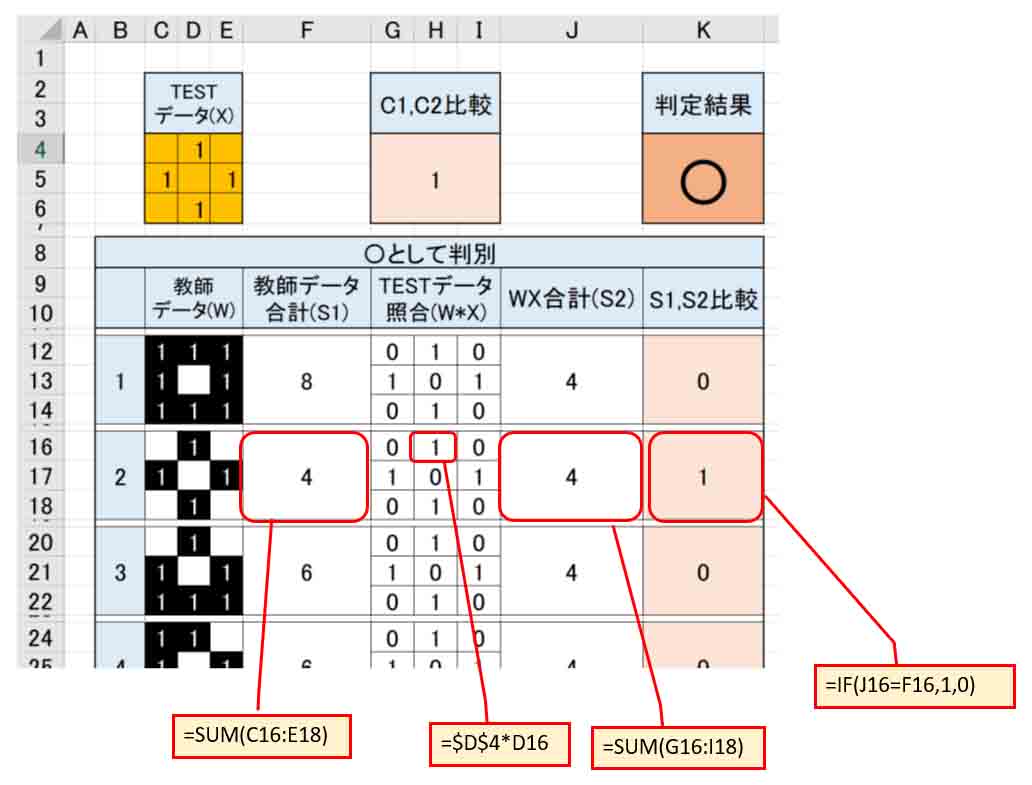
(図2_02)
赤枠の所にあるように、教師データの合計値(S1)を算出します。
そして、その隣にTESTデータ(X)と教師データ(W)の照合値として、TESTデータ(X)と教師データ(W)を掛けた値 W * X を9個算出しておきます。
TESTデータと教師データが双方1であれば、1を算出し、それ以外ならば0になります。
照合するなら、0と1の掛け算が便利ですね。
その隣に、W * X の合計値(S2)を算出します。
その隣にS1とS2を比較して、同じ値ならば1を、異なればゼロを表記するようにIF文を組みます。
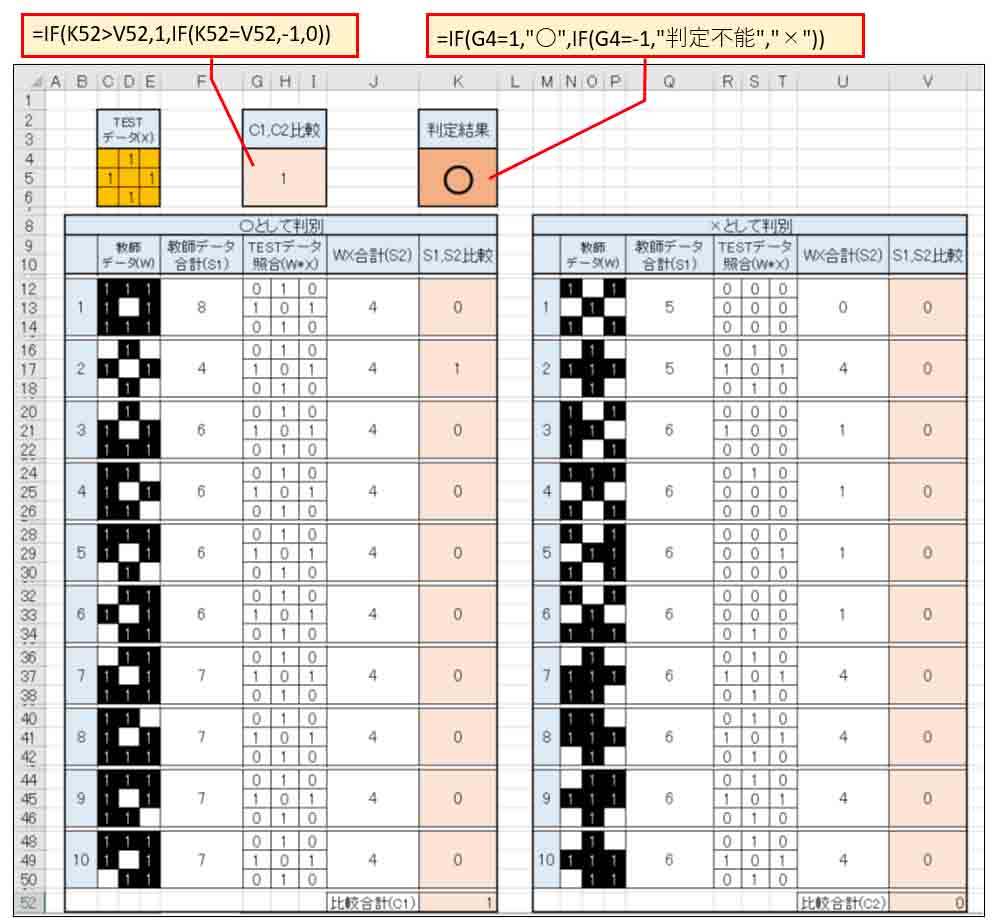
次に、下図の様に、○印としての判別データと、×印としての判別データを組みます。
S1とS2の比較値をそれぞれ合計して、C1、C2 という値を作って置き、下図の様に比較して
C1>C2
ならば、○として判定。
C1<C2 ならば×として判定。
C1=C2 ならば-1を出力し、「判定不能」と表記するようにします。
(図2_03)
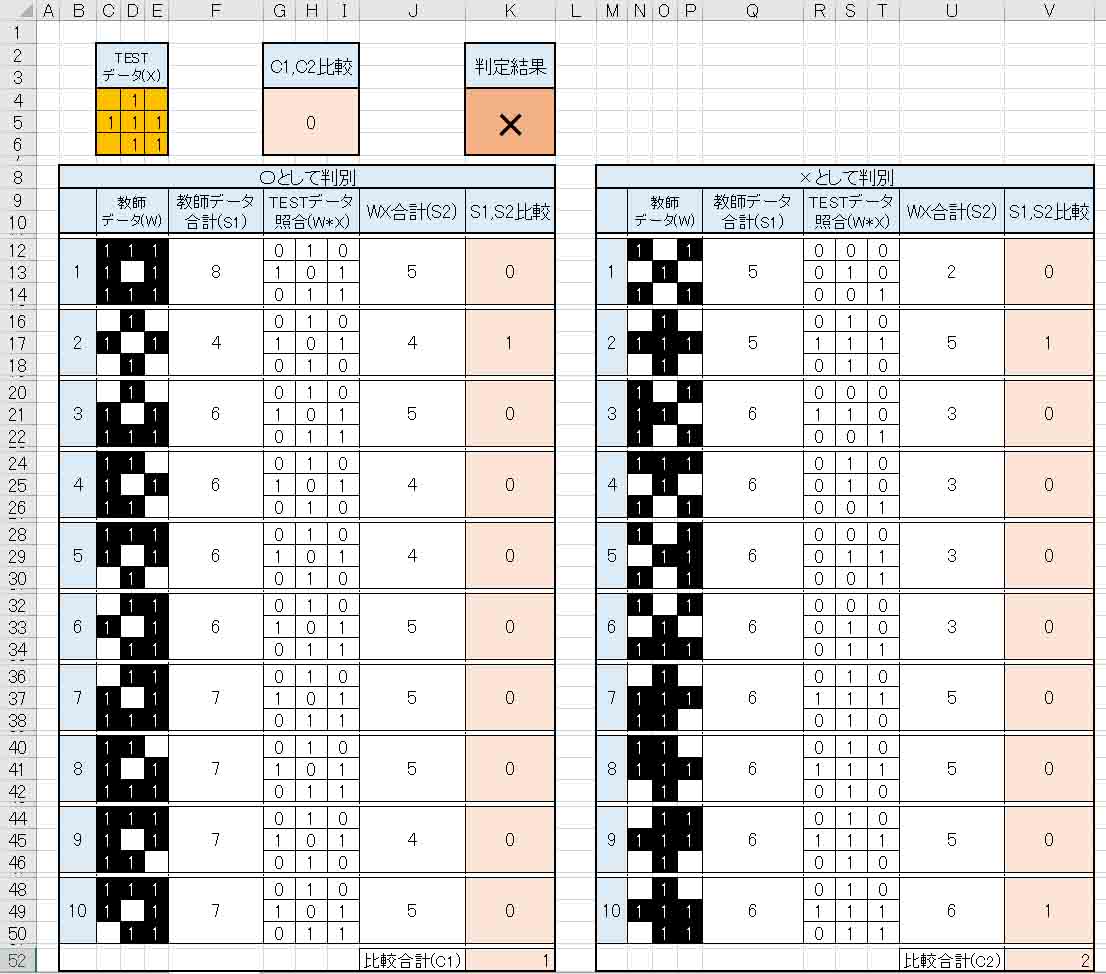
例えば、以下のようにTESTデータを入力すると、×と判定されます。
(図2_04)
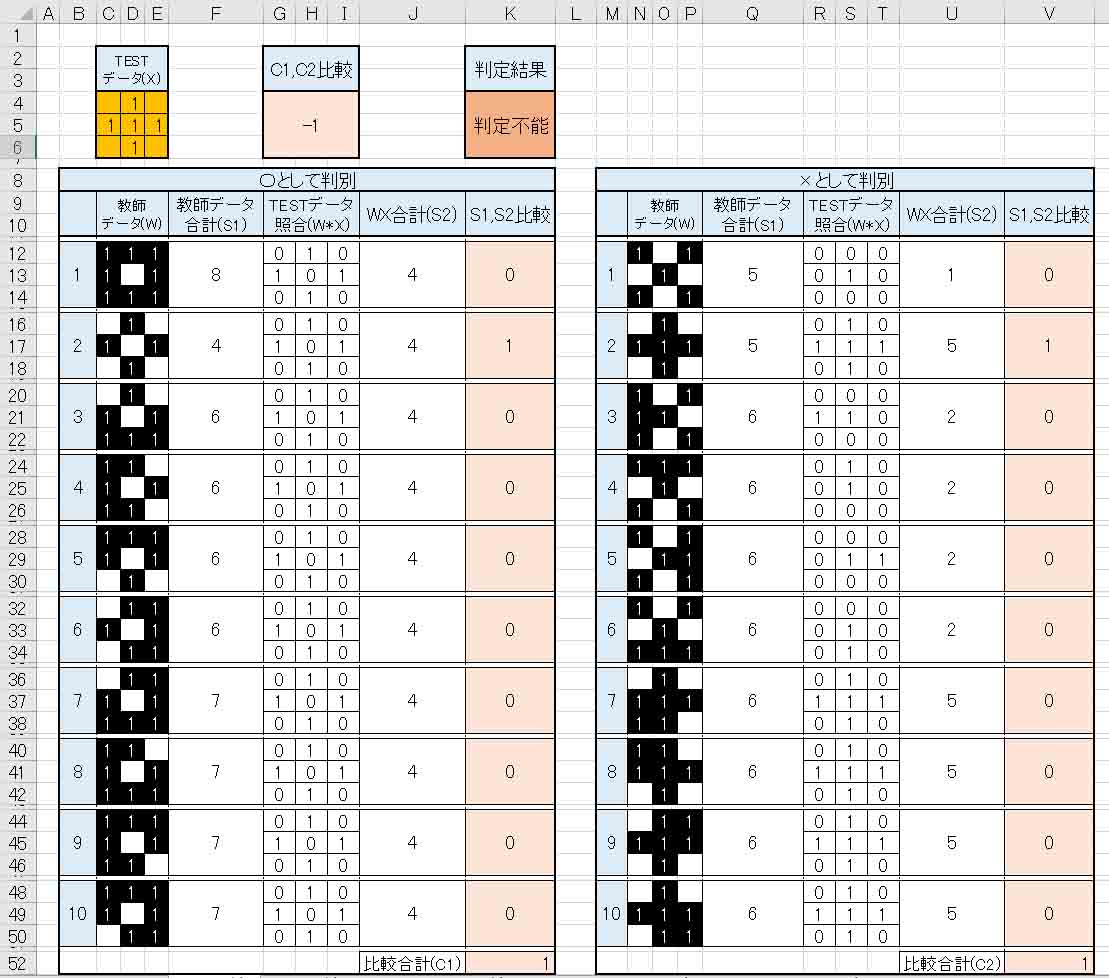
ただ、この自己流プログラムの場合、下図の様にTESTデータを入力すると、C1=C2 となってしまい、判定不能になってしまいます。
(図2_05)
本来ならこの場合、中央の画素がゼロなら○印、1ならば×印と判定する項目を設ければ正常な判定をすることができますね。
因みに一連の教師データに注目すると、○印は中央の画素は全てゼロ、×印の中央画素は全て1になっていることがわかります。
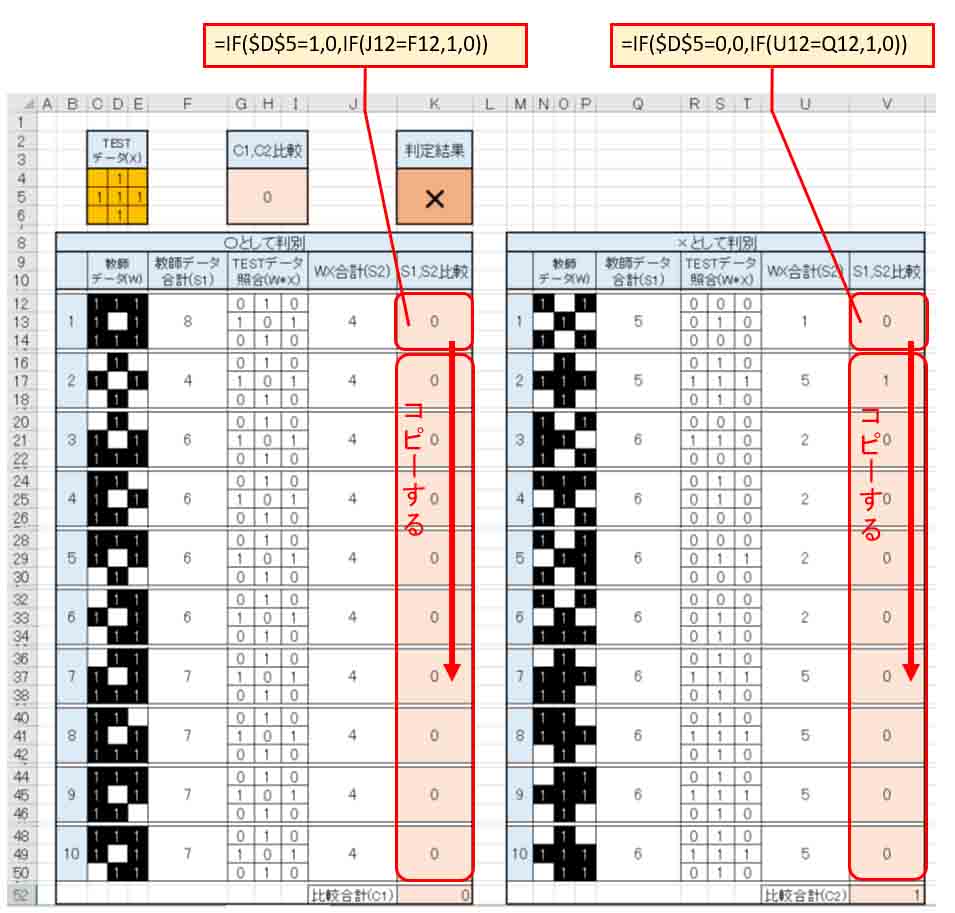
なら、ここではS1とS2の比較のところで、以下のようなIF文を設定し、その対象全セルについてコピペして反映しておきます。
(図2_06)
そうすると、正しく○と×が判定できるようになりました。
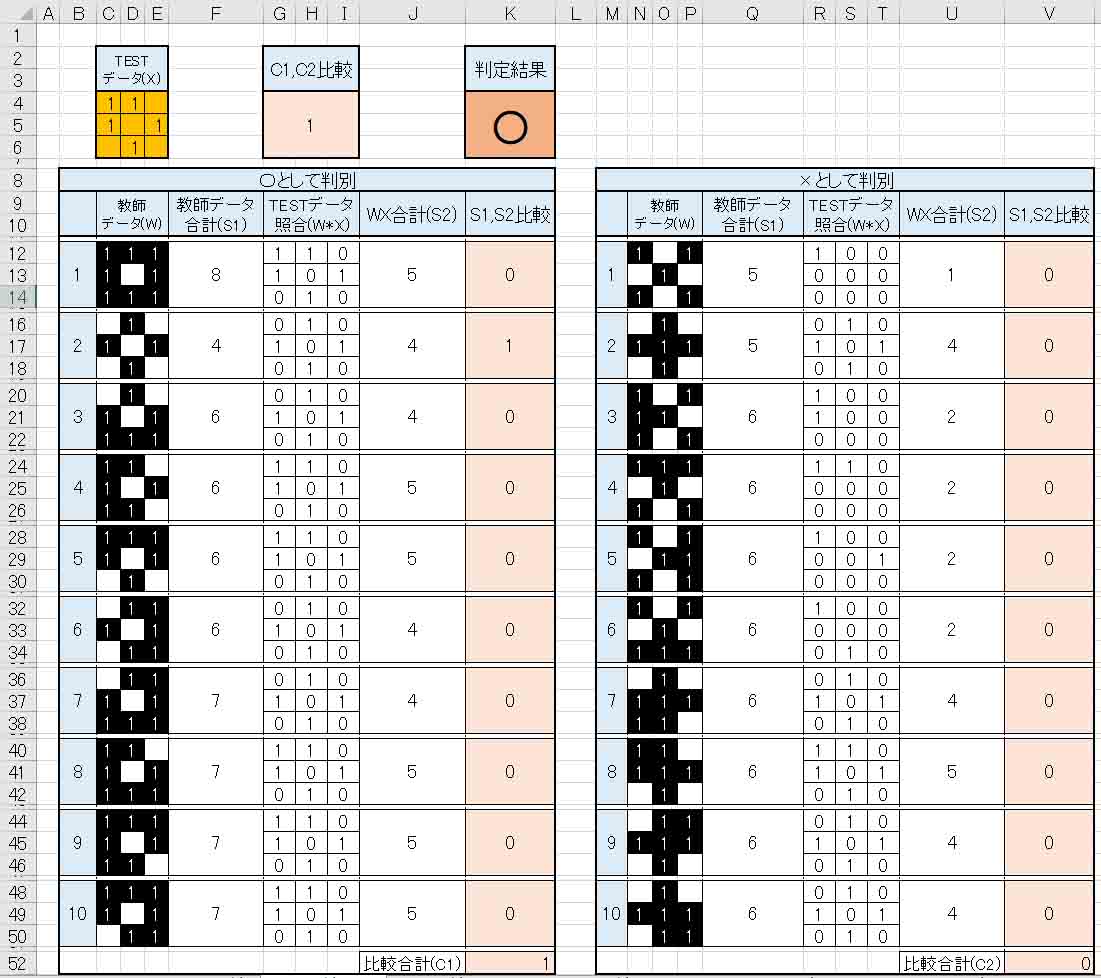
ところで、このプログラムで教師データには無い以下のTESTパターンを入力するとどうなるかというと、
(図2_07)
○印と判定してくれました。
これは誰が見ても○印だろうと判断すると思うので、たまたまラッキーでした。
ただ、下図の様なTESTデータの場合はどうなるのかな?
(図2_08)
これは、カメラ(イメージセンサ)を対象物から遠ざけて見た場合のデータと考えることができます。
この場合、人間が判断しても○か×かを判断できないので、正しい判断ですね。
ただ、これを○印として教師データに与えて、○印として判定させたい場合は、中央の画素が1となってしまうので、IF文条件分岐をいろいろと改良しなければなりません。
画素数が多くなると、この自己流プログラムではかなり複雑な条件分岐しなければならず、途方に暮れることが明らかですね。
自己流でIF文で構成していくと考えるとすると、複雑な画像はとうてい無理ですね。
では、ニューラルネットワークだったらこの問題を解決できるんでしょうか?
そう思って、書籍を勉強し始めると、書籍が余りに難しいので、早々に諦めてしまう罠にハマります。
なので、ここではとりあえずパッと書籍を見てかじっただけの知識で、いきなりバイアスとシグモイド関数を使ってみることにしました。
意味が解らなくても使ってみるんです。
3.自己流計算プログラムにバイアス(閾値)とシグモイド関数を取り入れてみる
では、自己流ではすぐに限界に達したので、先ほど紹介した書籍を斜め読みして知ったバイアス(閾値:しきいち)とシグモイド関数というものを組み込んでみます。
まず、ニューラルネットワークの書籍を読むと、結構初期の段階でバイアスとかシグモイド関数とか出てくると思います。
その時点で良く解らなくて、意味不明な専門用語が多くなってきて、私は本を閉じてしまいました。
でも、ここでは意味が解らなくてもとりあえず使ってみます。
ただ、バイアスについては、いきなり使おうとしてもどう使って良いか分からないので、自分流で理解したことを述べます。
バイアスは、いわゆる単なる閾値(しきい値)だと思えば良いのではないかと思います。
バイアスとだけ専門用語が羅列されているとサッパリ分からなくなりますね。
要するに以下のように、先ほどのエクセルデータのWX合計値がバイアス(閾値)以上になれば、1を出力するというようなことです。
W X合計値 > バイアス(閾値) ⇒ 1を出力
つまりは、
W X合計値 – バイアス(閾値) > 0 ⇒ 1を出力
としても同じ意味です。
バイアスについて、ニューラルネットワークの書籍で私がなかなか理解できなかったのは、式が
(WX1+WX2+WX3+……) + b > 0
とか書かれていることが多いことです。
「+b ってどういうこと???」
となりました。
ここが私は最初につまずいたところで、ややこしいところでした。
その点でいえば、先ほど紹介した書籍「Excelでわかるディープラーニング超入門」ではこのバイアスについてとても分かり易く書かれていて、初心者の私には理解の助けになりました。
要は、バイアスを入れた式は、
(WX1+WX2+WX3+……) + (- b) > 0
と同じことです。
bはΘと表現しているところもありますね。
つまりは、数学的に言うと、
(WX1+WX2+WX3+……) > b
という不等式があったら、右辺のbを左辺へ移項すれば、
(WX1+WX2+WX3+……) – b > 0
となるわけです。
要するに、バイアスはその値を超えたら、何かが動作すると覚えておけば良いのだと思います。
では、いままで作ってきた自己流計算プログラムでバイアス(閾値)をどう設定するかが問題です。
とりあえず、あまり深く考えずに、教師データの合計値をバイアス値としておきます。
ただ、バイアス値を設定しただけでは、判別結果については何も解決しないので、ここでシグモイド関数というものをとりあえず使ってみます。
ニューラルネットワークの参考書には必ずと言ってよいほど登場する謎の関数です。
シグモイド関数についてはネット上に沢山情報があるし、先ほど紹介した書籍にも書かれているので、ここでは説明を省略します。
要するに、入力にどんな値を入れても出力は0~1の間に収まるという関数です。
Excelの数式では、
=1/(1+EXP(-X))
となります。
Xのところにセル値を入力してやります。
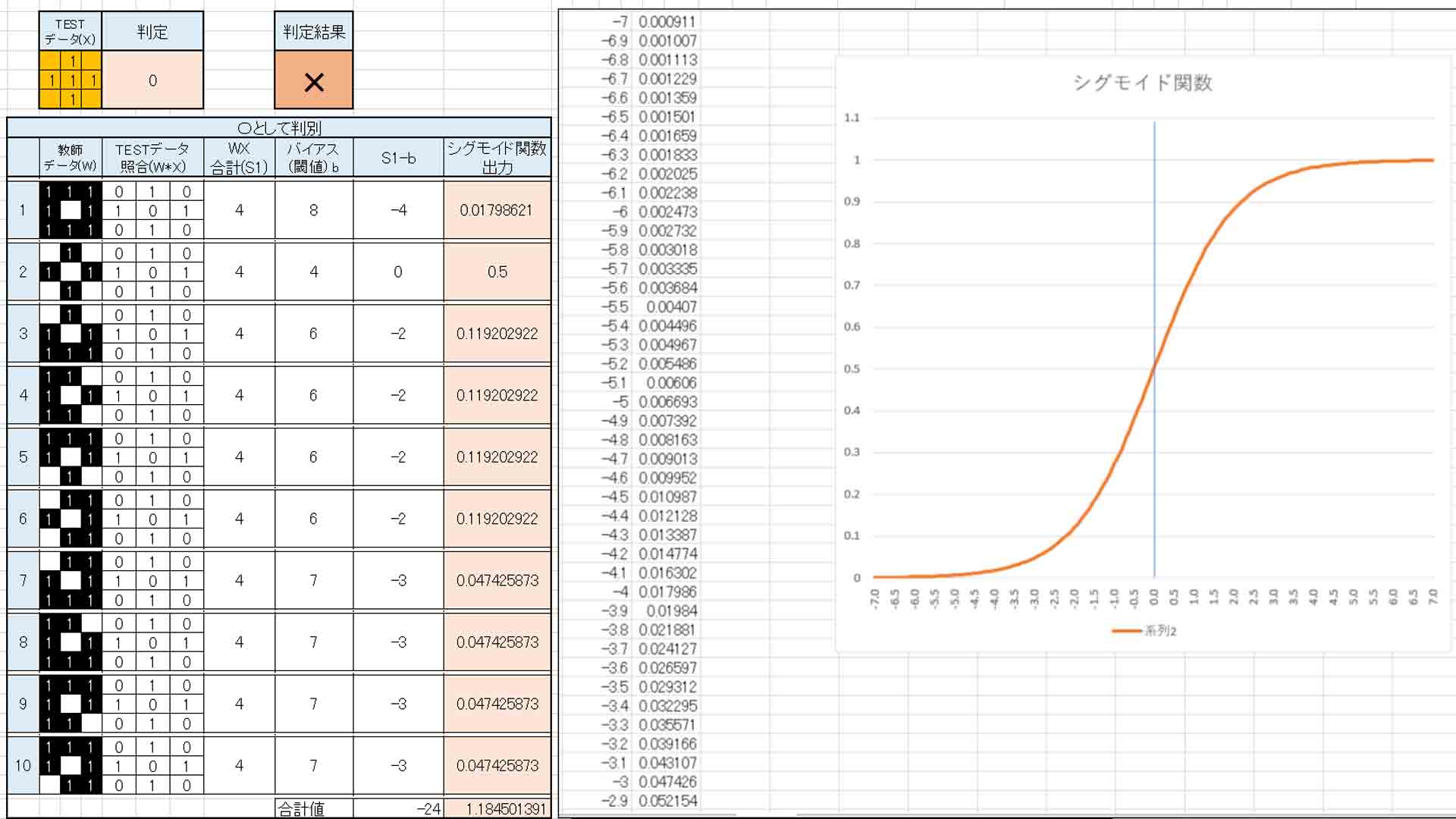
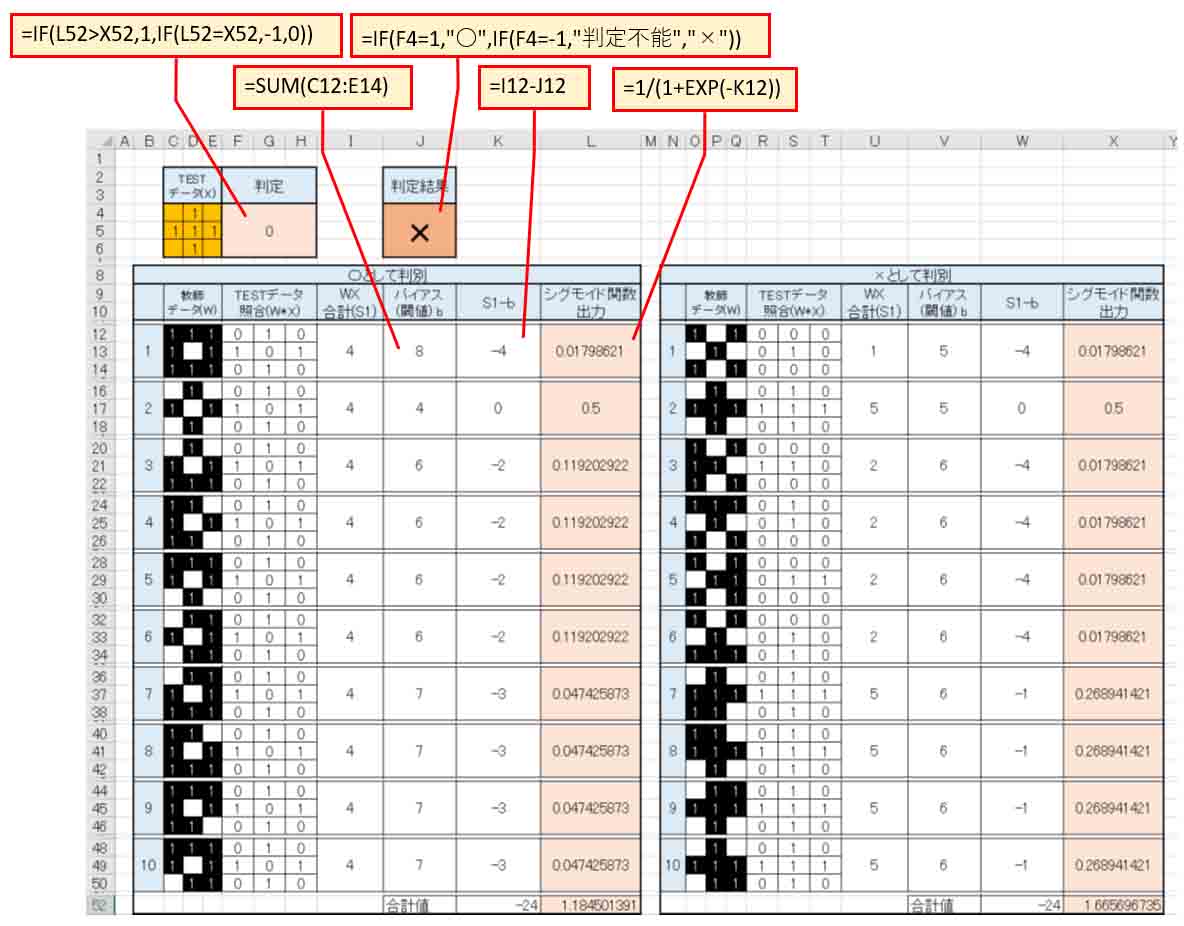
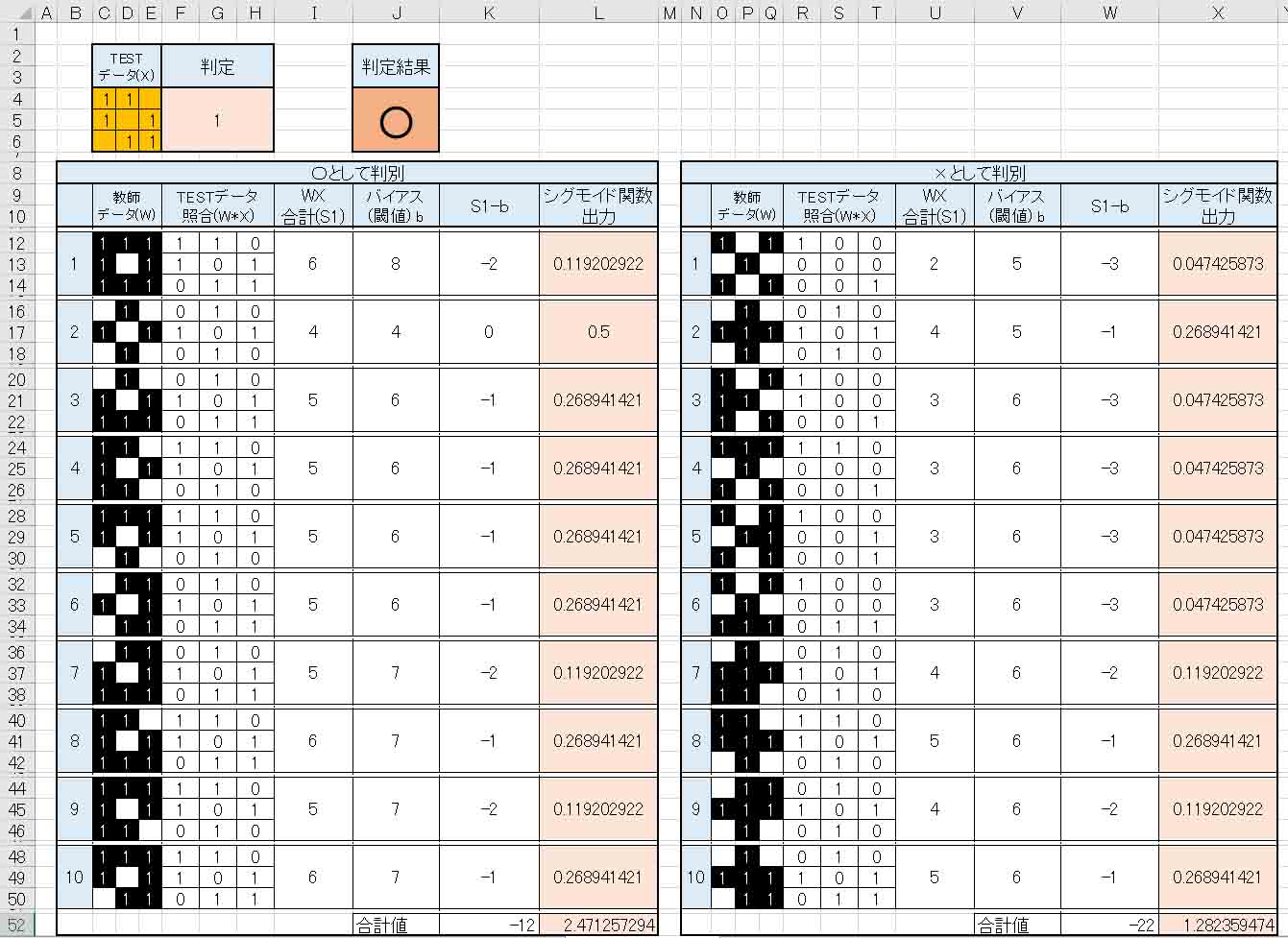
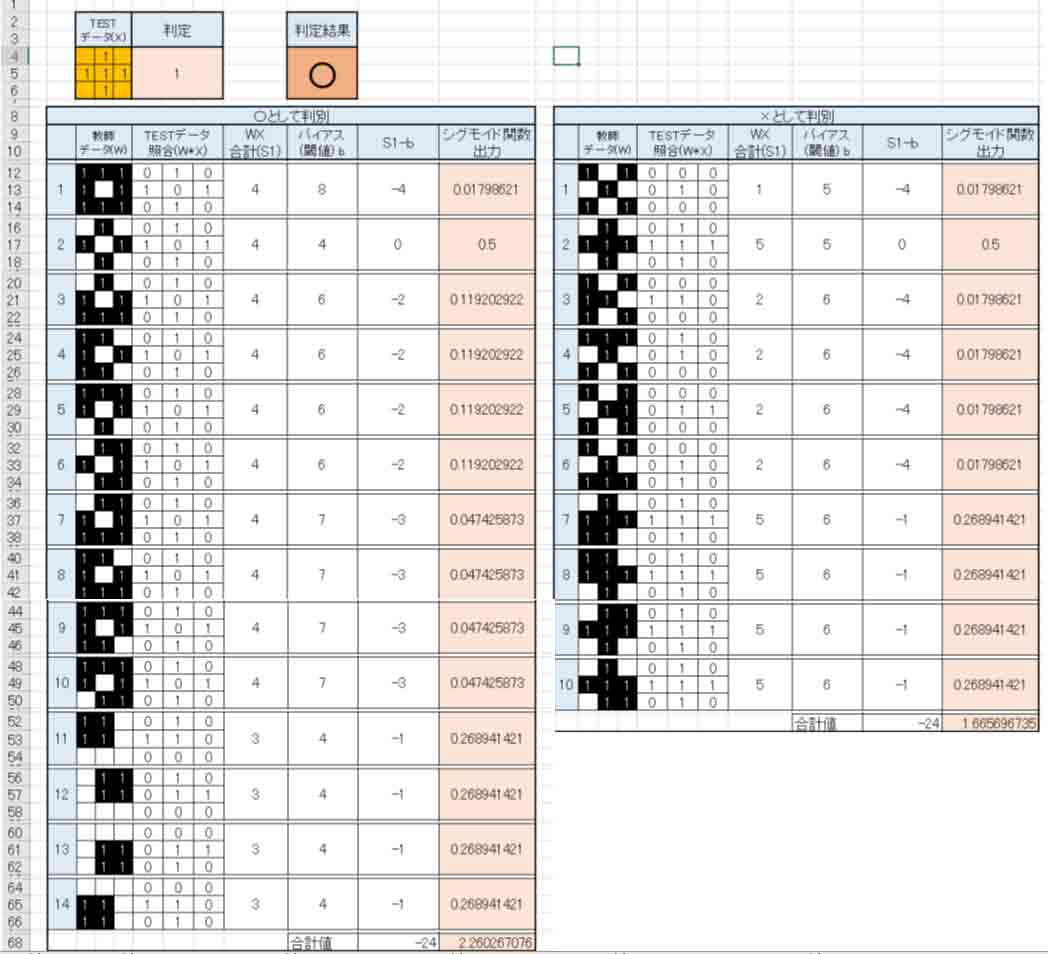
下図の様な感じにします。
(図3_01)
いい具合になりました。
(図2_05)では判定不能だったものが、シグモイド関数に変えただけで×印と判定してくれました。
ただ、実はこれはたまたまこうなっただけです。
これを見ると、
WX合計値(S1) = b
となった場合、シグモイド関数出力が0.5になります。
それと、面白いのは、(S1-b)の合計値が○と×で同じなのに、シグモイド関数出力の合計値が異なっています。
なぜ、そうなるのか?
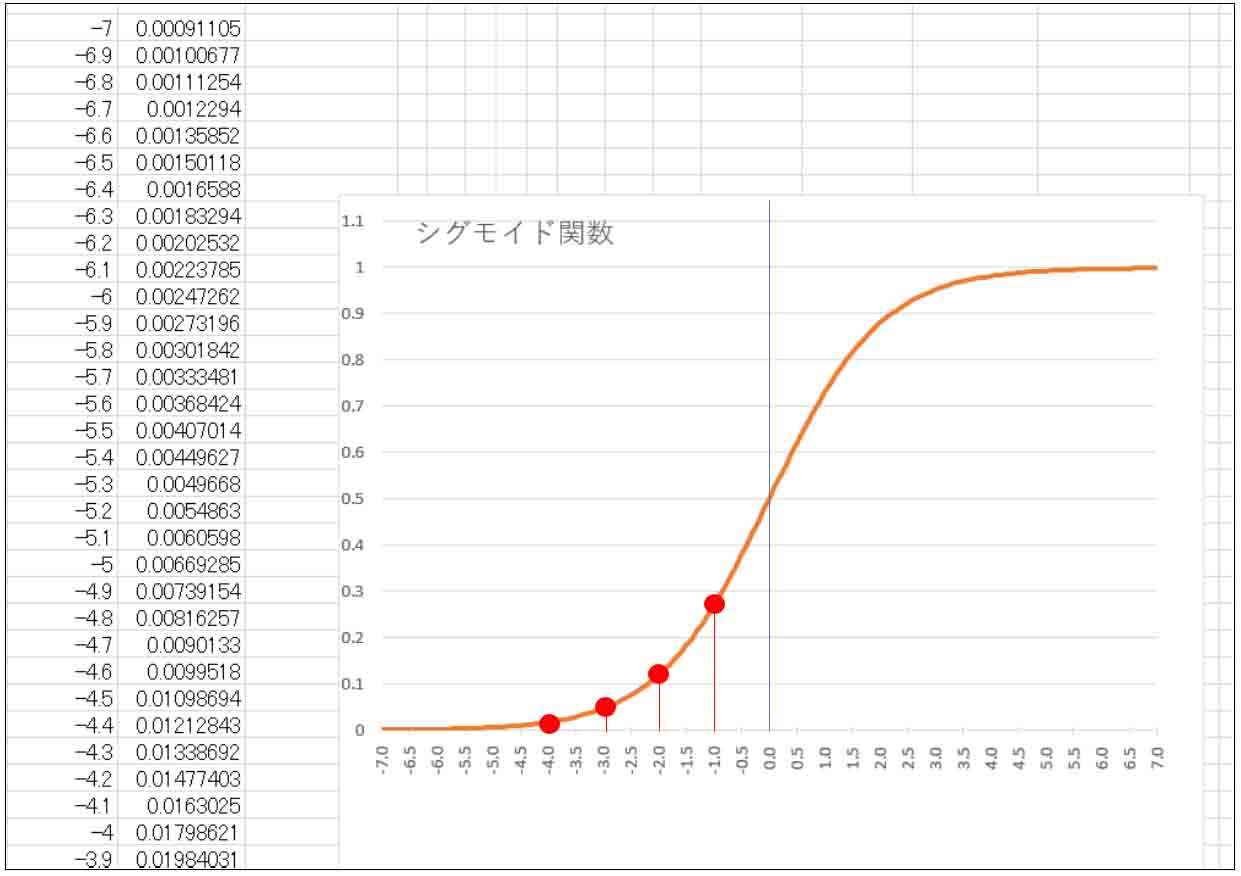
まず、Excelでシグモイド関数のグラフを作ってみました。
すると、下図の様な感じになりました。
(図3_02)
これから、赤い丸印のところを見てみると、横軸が-4.0から-3.0の間ではシグモイド関数出力はほんのちょっとしか増えないけど、-2.0から-1.0に変化するとき、シグモイド関数出力はかなりドーンと増えています。
これから考えると、(図3_01)で「S1-b」合計値が等しいのにシグモイド関数出力の合計値が異なるのは、「S1-b」合計値に-2や-3が多くても、-1が多い方がシグモイド関数出力の合計値はグーンと大きくなるという事だと思います。
以上からシグモイド関数を使う利点というのは、教師データの正解に近い入力データになればなるほど、出力が大きくなるというところです。
逆に正解から遠い値だと少ししか変化しないということです。
活性化関数という意味合いが良く解りました。
そして、シグモイド関数出力が0~1の間限定で出力するということは、そのまま確率表記できるし、そのままの値で確率計算ができるので便利ですね。
シグモイド関数が使われる意味が良く解りました。
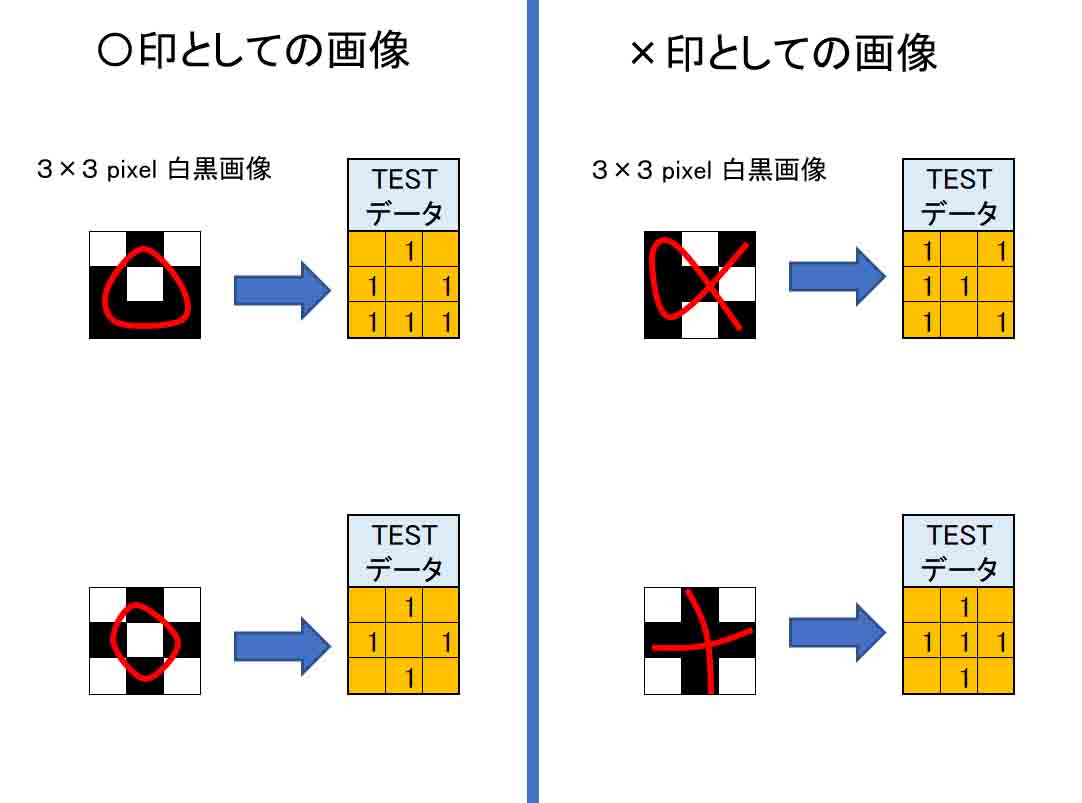
ところで、下図の様に教師データとして登録していない画像でも○印として判定してくれました。
これは、人間なら誰でも○印として判定すると思います。
(図3_03)
でも、これはあまり喜ぶところではなくて、たまたまそうなったというだけなんですけどね。
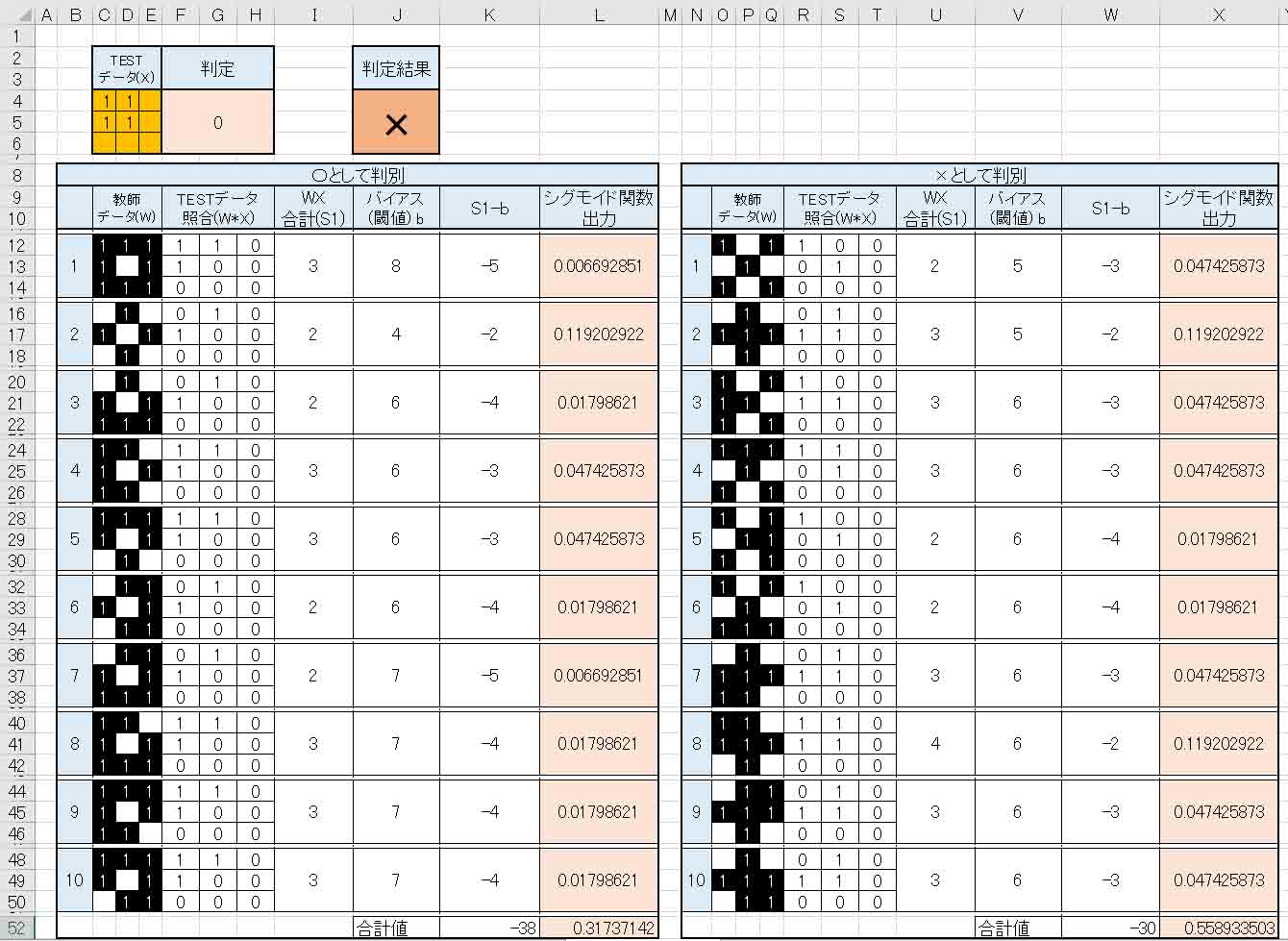
また、(図2_08)のところで入力したTESTデータと同じものを入力すると、下図の様に×印として判定されました。
(図3_04)
これを○印として判定させたい場合は、やはり条件分岐を新たに作らねばならないと思います。
シグモイド関数はただ単に出力を活性化させるだけなので、判定まではできませんね。
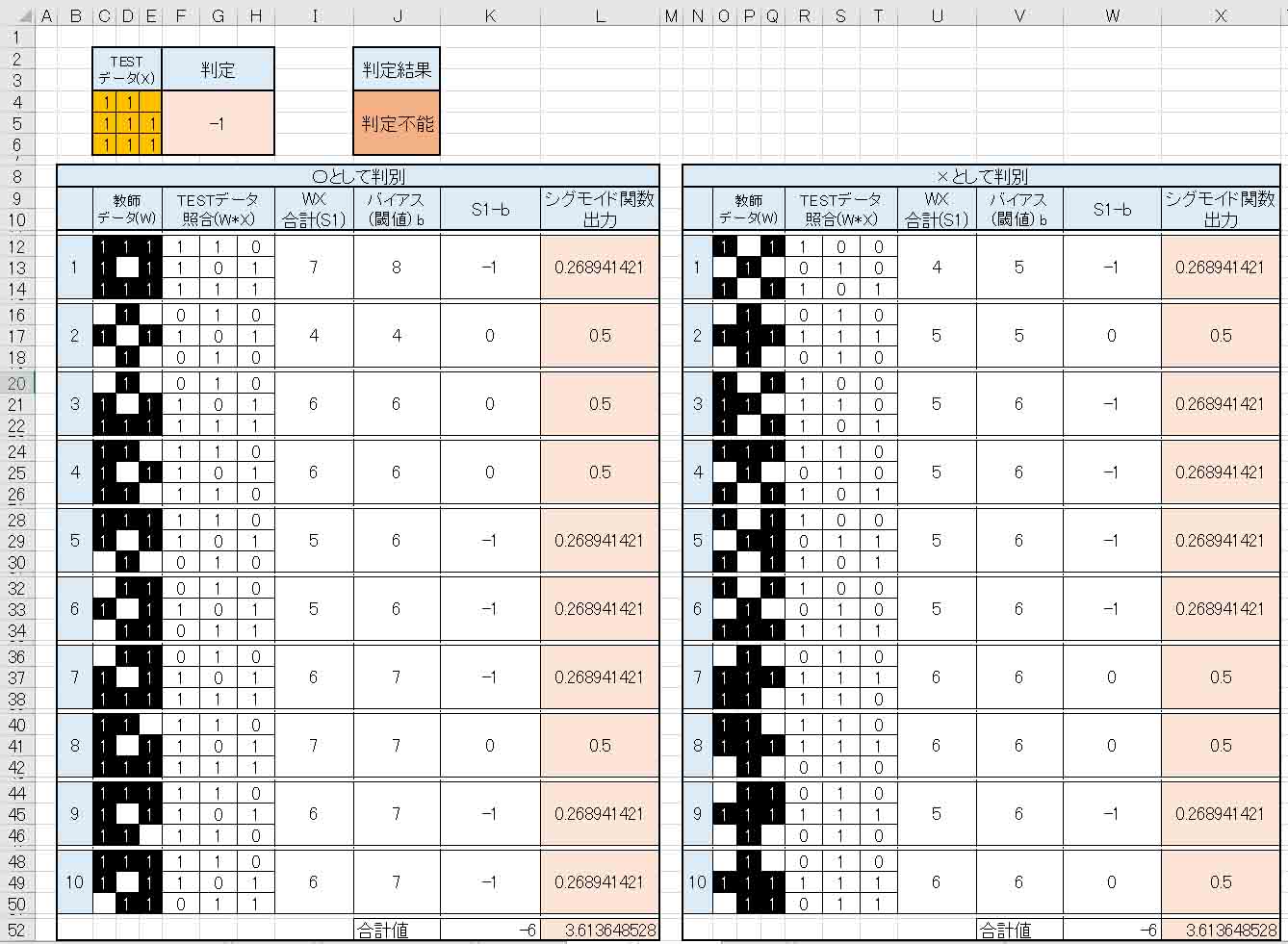
また、下図の様なTESTデータだと、判定不能と判断されました。
(図3_05)
やはり、いくらシグモイド関数を使っていたとしても、この少ないパラメータでは○印と×印の出力合計値がたまたまピッタリ一致してしまうことも有り得るわけですね。
そもそも、このTESTデータ自体、人間が見ても○か×かの判断はできませんけど。。。
以上から、個人的にニューラルネットワークでシグモイド関数というものが使われる理由が理解できたので、これからは積極的に使っていこうと思います。
4.自己流計算プログラムの限界
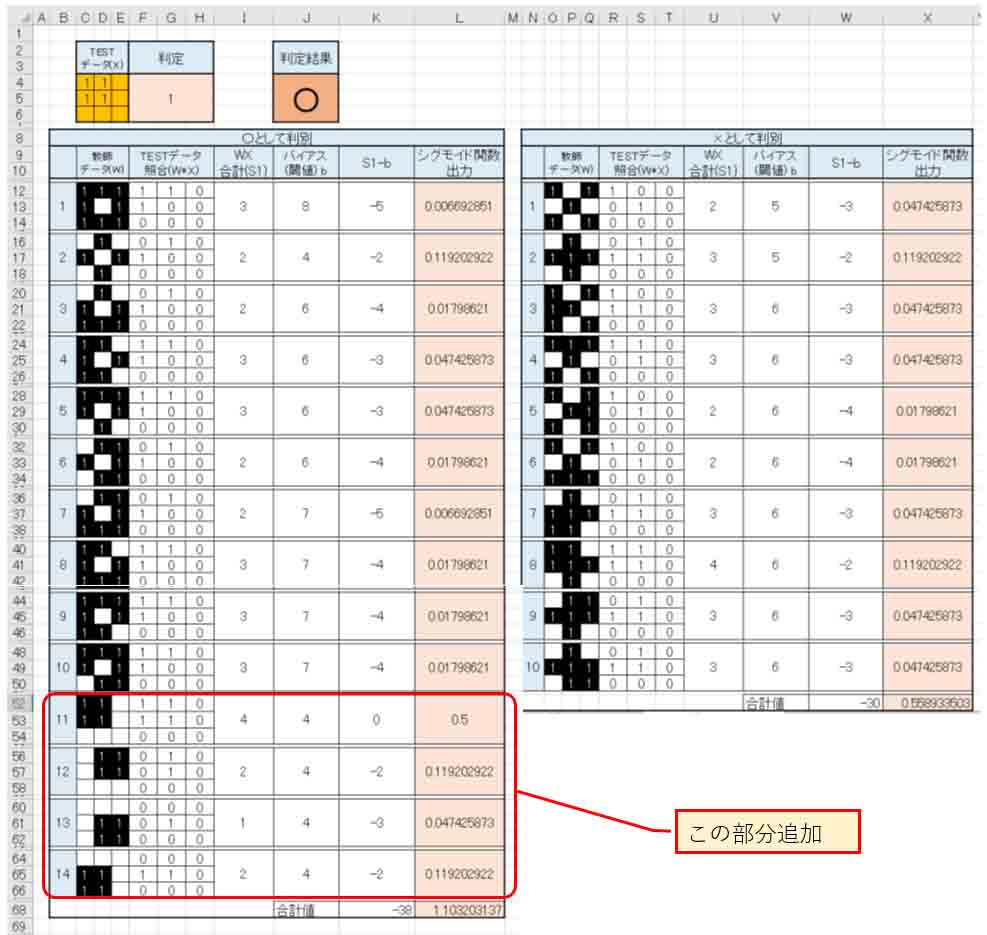
では、先ほどの(図3_01)で良い結果が得られたので、(図3_04)のようなTESTデータを入力しても○印と判定するように教師データを追加してみます。
下図の様な感じです。
(図4_01)
すると、○印と判定してくれました。
ただし!!!
分かる人はパッと見てこれは無駄だと思われると思います。
以下のようなTESTデータを入力すると、
(図4_02)
×として判定されなければならないはずの正常な判定ができなくなってしまいました。
考えてみれば当たり前と言えば当たり前です。
なぜなら、○印としてのシグモイド関数出力の合計値が×印よりも増加しているからです。
そりゃ、データを増やせば合計値も増えますがな。。。
同じ条件にするなら、×印としての教師データも4つ分増やす必要があることは明らかですね。
それならば、IF文条件分岐を多量に作って判定した方が確実ですね。
でも、それは単純で画素数が少ない画像の場合は良いですけど、もっと画素数が増えるとプログラミングが複雑化することは目に見えてしまいます。
以上から、画像認識を自己流計算プログラミングでやろうとするのは、自分の実力ではそもそも無理だと悟りました。
まとめ
以上、ニューラルネットワークやディープラーニングを始める前段階として、Excelで自己流計算式プログラムの限界と、バイアスやシグモイド関数の利点について探ってみました。
バイアスについては難しいことは無いのに、書籍によっては難解に思えてしまいますし、シグモイド関数が出てくると更に難しく感じます。
でも、バイアスは単なる閾値で、出力にはシグモイド関数を使った方が断然良いとだけ覚えておいて、次に進むと良いのではないかと思います。
ここまで来ると、スッとニューラルネットワークの勉強に入れると思います。
(あくまで個人的見解)
以上、今回はここまでです。
次回はいよいよニューラルネットワークをExcelで組んでみたいと思います。
ゆくゆくは、マイコンとイメージセンサで画像認識を実現してみたいと思います。
ではまた。。。
Amazon.co.jp 当ブログのおすすめ


コメント